 por RodriguesBruno » Qui Mai 22, 2014 18:26
por RodriguesBruno » Qui Mai 22, 2014 18:26
Olá, estou com certa dificuldade no exercício em anexo.
Neste exercício, tentei usar a fórmula

e

em que:
Tgx=Senx/Cosx
-3=Senx/Cosx
Senx=-3Cosx
Agora substituindo na fórmula 2:
![{Sen}^{2}x+{Cos}^{2}x=1
{3Cos}^{2}x+{Cos}^{2}x=1
{4Cos}^{2}x=1
{Cos}^{2}x=\frac{1}{4}
Cosx=\sqrt[2]{\frac{1}{4}} {Sen}^{2}x+{Cos}^{2}x=1
{3Cos}^{2}x+{Cos}^{2}x=1
{4Cos}^{2}x=1
{Cos}^{2}x=\frac{1}{4}
Cosx=\sqrt[2]{\frac{1}{4}}](/latexrender/pictures/05d93f19cfdc099ae9f01a8dd4ea352b.png)
Porém, esse não é o resultado e não sei nenhum outro modo de realizar esse exercício, por isso preciso de ajuda e agradeço desde já pela atenção.
Obs.:
GABARITO ABruno.
- Anexos
-

- Trig..PNG (8.2 KiB) Exibido 2075 vezes
-
RodriguesBruno
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Mai 20, 2014 18:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por RonnieAlmeida » Qui Mai 22, 2014 19:17
por RonnieAlmeida » Qui Mai 22, 2014 19:17
Vamos lá!
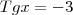
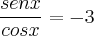
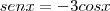
Elevando os dois membros ao quadrado:
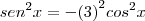
(1)
Por definição, temos:
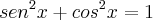
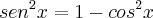
(2)
Então, substituindo (2) em (1):

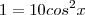
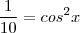
Após tirarmos as raízes dos dois membros, chegaremos em:
![cosx = + \sqrt[2]{10}/10 cosx = + \sqrt[2]{10}/10](/latexrender/pictures/3f442bd74a45541bf90e00299b0cb690.png)
ou
![cosx = - \sqrt[2]{10}/10 cosx = - \sqrt[2]{10}/10](/latexrender/pictures/bdc09a6911118e46c95cdd6023de8928.png)
Se x pertence ao 4º quadrante, então seu cosseno é obrigatoriamente positivo...
Portanto
![cosx = + \sqrt[2]{10}/10 cosx = + \sqrt[2]{10}/10](/latexrender/pictures/3f442bd74a45541bf90e00299b0cb690.png)
Alternativa
A
-
RonnieAlmeida
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Mai 22, 2014 16:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por RodriguesBruno » Sex Mai 23, 2014 15:30
por RodriguesBruno » Sex Mai 23, 2014 15:30
Fico muito grato por sua ajuda.
-
RodriguesBruno
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Mai 20, 2014 18:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (Trigonometria) problema trigonometria
por Luizap11 » Qui Dez 05, 2013 00:33
- 2 Respostas
- 5260 Exibições
- Última mensagem por Edunclec

Qui Dez 05, 2013 20:53
Trigonometria
-
- Problema de Trigonometria
por Dimas » Ter Nov 09, 2010 11:32
- 7 Respostas
- 5748 Exibições
- Última mensagem por Molina

Qui Jul 14, 2011 20:34
Trigonometria
-
- Trigonometria- Problema
por funtastic_lif » Sáb Out 06, 2012 09:30
- 2 Respostas
- 2071 Exibições
- Última mensagem por funtastic_lif

Sáb Out 06, 2012 14:14
Trigonometria
-
- Problema Trigonometria
por marinalcd » Dom Jun 11, 2017 16:58
- 0 Respostas
- 3226 Exibições
- Última mensagem por marinalcd

Dom Jun 11, 2017 16:58
Trigonometria
-
- Ajudem !! Trigonometria - problema ...
 por Lunn » Qua Mar 09, 2011 15:58
por Lunn » Qua Mar 09, 2011 15:58
- 2 Respostas
- 2241 Exibições
- Última mensagem por Lunn

Qua Mar 09, 2011 19:50
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e  em que:
em que:![{Sen}^{2}x+{Cos}^{2}x=1
{3Cos}^{2}x+{Cos}^{2}x=1
{4Cos}^{2}x=1
{Cos}^{2}x=\frac{1}{4}
Cosx=\sqrt[2]{\frac{1}{4}} {Sen}^{2}x+{Cos}^{2}x=1
{3Cos}^{2}x+{Cos}^{2}x=1
{4Cos}^{2}x=1
{Cos}^{2}x=\frac{1}{4}
Cosx=\sqrt[2]{\frac{1}{4}}](/latexrender/pictures/05d93f19cfdc099ae9f01a8dd4ea352b.png)


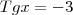
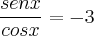
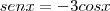
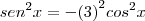 (1)
(1)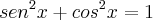
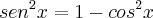 (2)
(2)
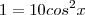
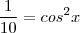
![cosx = + \sqrt[2]{10}/10 cosx = + \sqrt[2]{10}/10](/latexrender/pictures/3f442bd74a45541bf90e00299b0cb690.png) ou
ou ![cosx = - \sqrt[2]{10}/10 cosx = - \sqrt[2]{10}/10](/latexrender/pictures/bdc09a6911118e46c95cdd6023de8928.png)