O exercício é o seguinte:
Marcando no círculo trigonométrico as extremidades dos arcos da forma
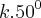 , k inteiro, obtemos os vértices de um polígono regular cujo número de lados é igual a:
, k inteiro, obtemos os vértices de um polígono regular cujo número de lados é igual a: Resposta: 36
Dúvidas:
Meu problema inicial é que não entendi direito o enunciado,
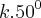 é o comprimento do arco?
é o comprimento do arco?Sei que os lados e os ângulos são congruentes e que
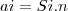

O diâmetro do círculo é a diagonal do polígono?
K seria o raio e
 o
o  ?
?Grata desde já!


 assim:
assim: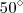 em
em  marcações, teremos um polígono regular de
marcações, teremos um polígono regular de  por
por 
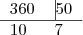
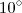 .
. .
. do polígono:
do polígono: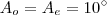
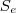 é (I):
é (I):



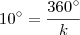
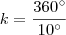
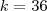

 é um ângulo central da circunferência
é um ângulo central da circunferência  de centro
de centro  .
. : ângulo interno
: ângulo interno

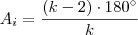
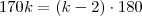

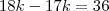
![\frac{\sqrt[]{3}}{2} \frac{\sqrt[]{3}}{2}](/latexrender/pictures/21682d7c1e802e9b52a99c01850489c4.png) com 0,5 (tanto positivo quando negativo). Já arrumei. Caso alguém tenha baixado, é só baixar o novo arquivo que está corrigido.
com 0,5 (tanto positivo quando negativo). Já arrumei. Caso alguém tenha baixado, é só baixar o novo arquivo que está corrigido.![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.