Tentei resolvê-la da seguinte forma;
Através do
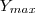e do 
obtive o valor do "a", que vale 1, porém, não sei como encontrar o valor do "b" para a conclusão da questão. Por dedução até consigo, entretanto, não sei demonstrar por meio da escrita. Por favor ajudem-me, desde já obrigado.
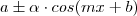
![Im=[a- \alpha,a+ \alpha]](/latexrender/pictures/34fed243ff855819d25634d182b52444.png "Im=[a- \alpha,a+ \alpha]")
![Im=[a- 1,a+ 1]](/latexrender/pictures/14cd1406b3c3c95cb37a58cf9307f951.png "Im=[a- 1,a+ 1]")
![[0,2]](/latexrender/pictures/70fd3f388413505934da60b43afc4088.png "[0,2]")
. Logo, 
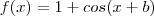, b por 
, quando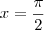 
temos que:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)