 por raimundoocjr » Seg Nov 08, 2010 23:05
por raimundoocjr » Seg Nov 08, 2010 23:05

Tentei resolvê-la da seguinte forma;
Através do
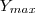
e do

obtive o valor do "a", que vale 1, porém, não sei como encontrar o valor do "b" para a conclusão da questão. Por dedução até consigo, entretanto, não sei demonstrar por meio da escrita.
Por favor ajudem-me, desde já obrigado.
-
raimundoocjr
-
 por Molina » Seg Nov 08, 2010 23:24
por Molina » Seg Nov 08, 2010 23:24
Boa noite.
Um macete que eu costumo usar pra questões deste tipo é esse:
Sendo
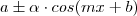
tem-se que a imagem é dada por:
![Im=[a- \alpha,a+ \alpha] Im=[a- \alpha,a+ \alpha]](/latexrender/pictures/34fed243ff855819d25634d182b52444.png)
Neste seu exercício temos que

Assim, a imagem é dada por
![Im=[a- 1,a+ 1] Im=[a- 1,a+ 1]](/latexrender/pictures/14cd1406b3c3c95cb37a58cf9307f951.png)
E a imagem pelo gráfico é
![[0,2] [0,2]](/latexrender/pictures/70fd3f388413505934da60b43afc4088.png)
. Logo,

Assim nos resta apenas as alternativas
(B) e
(D)Um simples teste, como por exemplo substituindo em
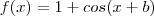
, b por

, quando
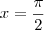
temos que:

E o que nos comprova que a alternativa correta é
(B).
Bom estudo!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por raimundoocjr » Ter Nov 09, 2010 13:29
por raimundoocjr » Ter Nov 09, 2010 13:29
Muito obrigado. Realmente, a substituição é a via mais curta.
-
raimundoocjr
-
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [trigonometria] trigonometria em triangulo qualquer
por biamassa00 » Sex Mai 25, 2012 22:19
- 0 Respostas
- 3596 Exibições
- Última mensagem por biamassa00

Sex Mai 25, 2012 22:19
Trigonometria
-
- (Trigonometria) problema trigonometria
por Luizap11 » Qui Dez 05, 2013 00:33
- 2 Respostas
- 5274 Exibições
- Última mensagem por Edunclec

Qui Dez 05, 2013 20:53
Trigonometria
-
- trigonometria
por Cleyson007 » Qua Set 24, 2008 19:44
- 2 Respostas
- 3415 Exibições
- Última mensagem por admin

Ter Set 30, 2008 19:08
Trigonometria
-
- trigonometria
por Micheline » Dom Jan 25, 2009 16:21
- 5 Respostas
- 4966 Exibições
- Última mensagem por Cleyson007

Seg Jan 26, 2009 17:27
Trigonometria
-
- Trigonometria
por Flavio » Sex Fev 13, 2009 21:29
- 5 Respostas
- 5125 Exibições
- Última mensagem por Molina

Seg Fev 16, 2009 01:53
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

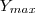 e do
e do  obtive o valor do "a", que vale 1, porém, não sei como encontrar o valor do "b" para a conclusão da questão. Por dedução até consigo, entretanto, não sei demonstrar por meio da escrita.
obtive o valor do "a", que vale 1, porém, não sei como encontrar o valor do "b" para a conclusão da questão. Por dedução até consigo, entretanto, não sei demonstrar por meio da escrita. 
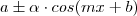
![Im=[a- \alpha,a+ \alpha] Im=[a- \alpha,a+ \alpha]](/latexrender/pictures/34fed243ff855819d25634d182b52444.png)

![Im=[a- 1,a+ 1] Im=[a- 1,a+ 1]](/latexrender/pictures/14cd1406b3c3c95cb37a58cf9307f951.png)
![[0,2] [0,2]](/latexrender/pictures/70fd3f388413505934da60b43afc4088.png) . Logo,
. Logo, 
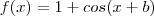 , b por
, b por  , quando
, quando 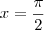 temos que:
temos que:

