 por Jhennyfer » Dom Ago 18, 2013 11:49
por Jhennyfer » Dom Ago 18, 2013 11:49
Oi pessoas...
boom a questão é a seguinte:
(UEPB) - Em 1614, o escocês John Napier (1550-1617) criou a ferramenta de calculo mais "afiada" que procedeu a invenção dos computadores, o logaritmo. Se
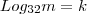
, então
![Log _{2}\sqrt[5]{m} Log _{2}\sqrt[5]{m}](/latexrender/pictures/d0e6c73acb053e481557591b65f00cce.png)
vale:
Bom tentei começando reduzindo o 32 a base 2...



e agora vem o meu problema (eu acho)...
![2=\sqrt[5]{m} 2=\sqrt[5]{m}](/latexrender/pictures/cc0ede511dc0aee33f85478da16d15ef.png)



Gabarito k...
esse calculo tá certo???
-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Dom Ago 18, 2013 12:52
por e8group » Dom Ago 18, 2013 12:52
As duas primeiras linhas de seu desenvolvimento estão corretas ,as demais etapas estão erradas.Como encontrou

? .
Note que
![32^k = m \iff 2^{5k} = m \iff (2^k)^5 =m \iff 2^k = \sqrt[5]{m} 32^k = m \iff 2^{5k} = m \iff (2^k)^5 =m \iff 2^k = \sqrt[5]{m}](/latexrender/pictures/4fa60ab8f7b46f84eb1601a5bafef58b.png)
. Aplicando o logaritmo de base 2 em ambos lados da igualdade obtém-se o que se pede no enunciado .De outra forma ,poderia começar "brincando " de multiplicar
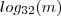
por
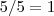
.veja a equivalência :
![log_{32}(m) = 1 \cdot log_{32}(m) = \frac{5}{5} \cdot log_{32}(m) = 5 (\frac{1}{5} log_{32}(m)) = 5 log_{32}(m^{1/5}) = 5 log_{32}(\sqrt[5]{m}) log_{32}(m) = 1 \cdot log_{32}(m) = \frac{5}{5} \cdot log_{32}(m) = 5 (\frac{1}{5} log_{32}(m)) = 5 log_{32}(m^{1/5}) = 5 log_{32}(\sqrt[5]{m})](/latexrender/pictures/6ed8a3ac9e5456d5e8517d60e1af0873.png)
.
Introduzindo a mudança de base para base 2 na última igualdade , segue :
![5 log_{32}(\sqrt[5]{m}) = 5 \frac{log_{2}(\sqrt[5]{m})}{log_2(32)} = ... 5 log_{32}(\sqrt[5]{m}) = 5 \frac{log_{2}(\sqrt[5]{m})}{log_2(32)} = ...](/latexrender/pictures/23be7244fdffa5eec46b17fea56430f1.png)
tente concluir e comente as dúvidas .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Jhennyfer » Dom Ago 18, 2013 13:32
por Jhennyfer » Dom Ago 18, 2013 13:32
Oi santhiago, entãoo...
isso acabou entrando em uma dúvida q eu coloquei em outro tópico, fiz uma bagunça aqui e não consegui concluir dessa maneira =/
mas...
ali onde chegamos em que:
![2^k=\sqrt[5]{m} 2^k=\sqrt[5]{m}](/latexrender/pictures/fdeee196aeeddfd89f55c923494d3263.png)
não podemos substituir em
![Log_2\sqrt[5]{m} Log_2\sqrt[5]{m}](/latexrender/pictures/1060dbfe119625cc70f1c15e5da195d2.png)
????
assim...



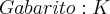
-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Dom Ago 18, 2013 14:29
por e8group » Dom Ago 18, 2013 14:29
Jhennyfer escreveu:Oi santhiago, entãoo...
isso acabou entrando em uma dúvida q eu coloquei em outro tópico, fiz uma bagunça aqui e não consegui concluir dessa maneira =/
mas...
ali onde chegamos em que:
![2^k=\sqrt[5]{m} 2^k=\sqrt[5]{m}](/latexrender/pictures/fdeee196aeeddfd89f55c923494d3263.png)
não podemos substituir em
![Log_2\sqrt[5]{m} Log_2\sqrt[5]{m}](/latexrender/pictures/1060dbfe119625cc70f1c15e5da195d2.png)
????
assim...



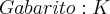
É isso mesmo ,está correto .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Jhennyfer » Dom Ago 18, 2013 16:00
por Jhennyfer » Dom Ago 18, 2013 16:00
Obrigado Santhiago...
Mas como eu havia dito, ainda tenho dúvidas nesse outro tipo de resolução que você deixou
santhiago escreveu:Introduzindo a mudança de base para base 2 na última igualdade , segue :
![5.\frac{Log_2\sqrt[5]{m}}{Log_232} 5.\frac{Log_2\sqrt[5]{m}}{Log_232}](/latexrender/pictures/5c3e5673810e1c0209004e54ac99e824.png)
...
tente concluir e comente as dúvidas .
Será q você pode me ajudar respondendo a questão q eu deixei nesse outro link:
viewtopic.php?f=108&t=12758Não é exatamente a mesma coisa, mas acho q pode acabar com muitas dúvidas q ainda tenho.
-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Juros] Não acho o tempo, não sei se estou fazendo certo
por AlexandreLuna » Ter Abr 24, 2012 20:46
- 3 Respostas
- 2927 Exibições
- Última mensagem por DanielFerreira

Qui Abr 26, 2012 20:10
Matemática Financeira
-
- ja tentei resolver e nada
por Sana2306 » Seg Set 21, 2009 14:43
- 2 Respostas
- 2171 Exibições
- Última mensagem por DanielFerreira

Sáb Set 26, 2009 12:18
Logaritmos
-
- Seno e cosseno de um arco trigonométrico, eu tentei resolver
por wesley_enrique » Dom Ago 08, 2010 19:38
- 6 Respostas
- 7695 Exibições
- Última mensagem por Pedro123

Seg Ago 09, 2010 18:59
Trigonometria
-
- tentei varias vezes ..mas ñ consegui resolver esses exercici
por ri20do » Seg Dez 15, 2008 00:03
- 1 Respostas
- 2657 Exibições
- Última mensagem por Molina

Ter Dez 16, 2008 16:47
Matemática Financeira
-
- Eu tentei, tentei e não consegui...
por phelipe » Seg Fev 08, 2010 12:40
- 4 Respostas
- 4862 Exibições
- Última mensagem por Elcioschin

Ter Fev 09, 2010 08:26
Desafios Médios
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
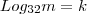 , então
, então ![Log _{2}\sqrt[5]{m} Log _{2}\sqrt[5]{m}](/latexrender/pictures/d0e6c73acb053e481557591b65f00cce.png) vale:
vale:


![2=\sqrt[5]{m} 2=\sqrt[5]{m}](/latexrender/pictures/cc0ede511dc0aee33f85478da16d15ef.png)





![32^k = m \iff 2^{5k} = m \iff (2^k)^5 =m \iff 2^k = \sqrt[5]{m} 32^k = m \iff 2^{5k} = m \iff (2^k)^5 =m \iff 2^k = \sqrt[5]{m}](/latexrender/pictures/4fa60ab8f7b46f84eb1601a5bafef58b.png) . Aplicando o logaritmo de base 2 em ambos lados da igualdade obtém-se o que se pede no enunciado .De outra forma ,poderia começar "brincando " de multiplicar
. Aplicando o logaritmo de base 2 em ambos lados da igualdade obtém-se o que se pede no enunciado .De outra forma ,poderia começar "brincando " de multiplicar 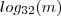 por
por 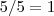 .veja a equivalência :
.veja a equivalência : ![log_{32}(m) = 1 \cdot log_{32}(m) = \frac{5}{5} \cdot log_{32}(m) = 5 (\frac{1}{5} log_{32}(m)) = 5 log_{32}(m^{1/5}) = 5 log_{32}(\sqrt[5]{m}) log_{32}(m) = 1 \cdot log_{32}(m) = \frac{5}{5} \cdot log_{32}(m) = 5 (\frac{1}{5} log_{32}(m)) = 5 log_{32}(m^{1/5}) = 5 log_{32}(\sqrt[5]{m})](/latexrender/pictures/6ed8a3ac9e5456d5e8517d60e1af0873.png) .
.![5 log_{32}(\sqrt[5]{m}) = 5 \frac{log_{2}(\sqrt[5]{m})}{log_2(32)} = ... 5 log_{32}(\sqrt[5]{m}) = 5 \frac{log_{2}(\sqrt[5]{m})}{log_2(32)} = ...](/latexrender/pictures/23be7244fdffa5eec46b17fea56430f1.png) tente concluir e comente as dúvidas .
tente concluir e comente as dúvidas .
![2^k=\sqrt[5]{m} 2^k=\sqrt[5]{m}](/latexrender/pictures/fdeee196aeeddfd89f55c923494d3263.png)
![Log_2\sqrt[5]{m} Log_2\sqrt[5]{m}](/latexrender/pictures/1060dbfe119625cc70f1c15e5da195d2.png) ????
????


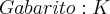
![5.\frac{Log_2\sqrt[5]{m}}{Log_232} 5.\frac{Log_2\sqrt[5]{m}}{Log_232}](/latexrender/pictures/5c3e5673810e1c0209004e54ac99e824.png) ...
...

 , avisa que eu resolvo.
, avisa que eu resolvo.

