Eu consegui montar. Ficou assim:
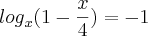
=

invertir a fração
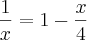
passei o "x" multiplicando e caí em uma equação do segundo grau

coloquei o "x" em evidência
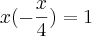
 e multipliquei por (-1)
e multipliquei por (-1)
só que não confere no gabarito. Eu não estou conseguindo resolver quando tem que achar a base.
Podem por favor me ajudar?
Obrigada e no aguardo
(fonte: Matemática aula por aula vol. único., pág. 157, Benigno Barreto Filho e Claudio Xavier da Silva)


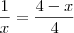
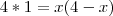
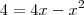
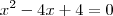








![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)