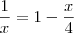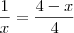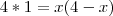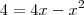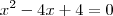por _Liilo » Dom Out 31, 2010 19:43
por _Liilo » Dom Out 31, 2010 19:43
Determinar a base na qual o logaritmo de 1- a quarta parte da base é igual a -1. (gabarito: 2)
Eu consegui montar. Ficou assim:
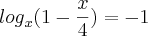
=

invertir a fração
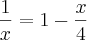
passei o "x" multiplicando e caí em uma equação do segundo grau

coloquei o "x" em evidência
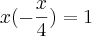

e multipliquei por (-1)

só que não confere no gabarito. Eu não estou conseguindo resolver quando tem que achar a base.
Podem por favor me ajudar?
Obrigada e no aguardo
(fonte: Matemática aula por aula vol. único., pág. 157, Benigno Barreto Filho e Claudio Xavier da Silva)
-
_Liilo
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Out 31, 2010 18:23
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: técnico em webdesign
- Andamento: formado
 por Molina » Dom Out 31, 2010 20:04
por Molina » Dom Out 31, 2010 20:04
Boa noite, Lilo.
Seu erro esta aqui:
_Liilo escreveu:passei o "x" multiplicando e caí em uma equação do segundo grau

Acho melhor você fazer assim:
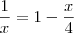
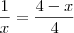
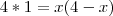
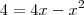
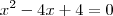
agora é só resolver e encontrar a resposta correta.
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por _Liilo » Dom Out 31, 2010 22:12
por _Liilo » Dom Out 31, 2010 22:12
Boa noite, Molina.
Deu tudo certo, muito obrigada

Confesso que demorei pra entender o 4 e o "x" passando multiplicando ao mesmo tempo
Tô colocando a equação só ficar completo o exercício.
Mais uma vez obrigada ^^





resposta no gabarito: confere
-
_Liilo
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Out 31, 2010 18:23
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: técnico em webdesign
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Logaritmo de base E
por Moreno1986 » Sex Ago 13, 2010 14:41
- 0 Respostas
- 729 Exibições
- Última mensagem por Moreno1986

Sex Ago 13, 2010 14:41
Logaritmos
-
- calculando logaritmo - mudando a base
por apotema2010 » Seg Mar 08, 2010 11:21
- 3 Respostas
- 2646 Exibições
- Última mensagem por MarceloFantini

Ter Mar 09, 2010 19:23
Logaritmos
-
- Logaritmo que base e logaritmando não são divisiveis iguais
por Linuxmh » Qua Jul 17, 2013 20:15
- 4 Respostas
- 3499 Exibições
- Última mensagem por Linuxmh

Sex Jul 19, 2013 12:01
Logaritmos
-
- [Lógica Digital] Sistema Numérico Conversão Base X - Base 10
por Luc4sPaulo » Sex Fev 17, 2017 12:32
- 0 Respostas
- 4162 Exibições
- Última mensagem por Luc4sPaulo

Sex Fev 17, 2017 12:32
Lógica
-
- [Base] Encontrar uma base e a dimensão do subespaço
por anderson_wallace » Sex Jan 10, 2014 00:48
- 3 Respostas
- 13858 Exibições
- Última mensagem por Guilherme Pimentel

Qua Jan 15, 2014 05:23
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
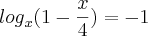

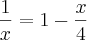

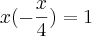
 e multipliquei por (-1)
e multipliquei por (-1)