Olá, como vão ?
Seguinte. Desenvolvi um programa para a faculdade para controlar um motor de passo.
É o seguinte : para completar uma volta ele dá 12 passos. Não é possivel dar passos fracionados.
Então 360 = 12 , 180 = 6, 90 = 3.
Preciso de uma função que qualquer grau que a pessoa colocar(147 por exemplo) ele seja convertido em passos e arredondado(para cima ou para baixo tanto faz).
Será que alguem da conta de resolver isso ?
o número de graus, e 
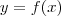o maior número inteiro de passos que não excede a taxa de conversão, então:
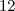passos, então 
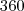º
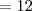passos e, portanto, 
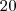º
passo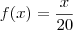 
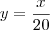, se 
, será o número de passos que o motor dará. Caso contrário, o resultado será entendido apenas como a parte inteira do número decimal que estará no quociente e assim o número de passos é arredonado para baixo.
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.