 por Ricardogferreira » Seg Jul 23, 2012 21:19
por Ricardogferreira » Seg Jul 23, 2012 21:19
Boa noite.
Não tenho dificuldade em representar graficamente uma função analisando a sua expressão algébrica. No entanto, não consigo executar em sentido contrário, ou seja, olhando o gráfico para descobrir a expressão.
Agradecia ajuda nos seguintes exemplos, por forma a deixar de ter dificuldades neste tipo de exercício (estão em causa funções quadráticas):
dados fornecidos no gráfico A (concavidade para baixo) - Xv: -1 Raízes: -2 e 0; Yv: 2 - Solução: f(x) = -2 (x+1)^2 + 2
dados fornecidos no gráfico B (concavidade para cima)- Xv: 2; Yv: 1; Gráfico corta o eixo Y em 3, no sentido decrescente - Solução: g(x) = 1/2 (x-2)^2 + 1
dados fornecidos no gráfico C (concavidade para cima)- Raízes: -1 e 3; Gráfico corta o eixo Y em -2, no sentido decrescente - Solução: h(x) = 2/3 (x-1)^2 - 8/3
Volto a referir que consigo construir o gráfico com os dados referentes à expressão algébrica. O que não consigo fazer é olhar para o gráfico daquelas funções e escrever a referida expressão.
Muito obrigado.
Ricardo
-
Ricardogferreira
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Jan 23, 2012 21:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Seg Jul 23, 2012 23:04
por MarceloFantini » Seg Jul 23, 2012 23:04
Mostre os gráficos, por favor. É importante notar também que, dado um gráfico qualquer, não é possível inferir que regra que gerou tal gráfico, apenas em casos muito específicos, como parábolas.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Ricardogferreira » Qui Jul 26, 2012 21:03
por Ricardogferreira » Qui Jul 26, 2012 21:03
Infelizmente não consegui anexar a imagem (não permite formato pdf). Os gráficos são gráficos de parábolas. O exercício vem no meu manual. Se puder me ajudar com essa informação, ótimo. Se não for possível, agradeço também.
-
Ricardogferreira
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Jan 23, 2012 21:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Qui Jul 26, 2012 21:59
por DanielFerreira » Qui Jul 26, 2012 21:59
Ricardo,
seja bem-vindo!
Resolverei o "gráfico A" tentando ser o mais claro possível, mas se ficar com dúvidas, não exite em perguntar, ok?!
Quanto as fórmulas:Sabemos que uma função quadrática é dada por

Sabemos também que

e
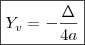 Quanto as conclusões:
Quanto as conclusões:Se as concavidade está voltada para baixo, podemos concluir que

Uma das raízes é nula, então, temos que
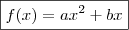
Logo,
 Quanto aos cálculos:
Quanto aos cálculos:I)
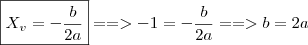
II)

Substituindo I) em II):
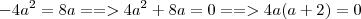
Como

temos

, com isso,

Logo,
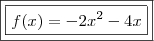
Espero ter ajudado!
Tente as outras e poste como fez.
Até logo,
Daniel F.
Editado pela última vez por
DanielFerreira em Sáb Jul 28, 2012 15:09, em um total de 1 vez.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por LuizAquino » Sex Jul 27, 2012 21:13
por LuizAquino » Sex Jul 27, 2012 21:13
Ricardogferreira escreveu:Infelizmente não consegui anexar a imagem (não permite formato pdf). Os gráficos são gráficos de parábolas. O exercício vem no meu manual.
Uma dica: você pode usar a tecla
Print Screen para copiar a sua tela. Em seguida, basta colar a imagem em um programa de edição e recortar a parte desejada. Após salvar esta imagem, basta anexá-la a sua mensagem usando os passos descritos no tópico:
[Anexos] Envio de anexosviewtopic.php?f=134&t=7460
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Ricardogferreira » Dom Jul 29, 2012 09:22
por Ricardogferreira » Dom Jul 29, 2012 09:22
Obrigado Daniel,
Desculpe incomodar novamente. Compreendi a sua explicação, mas fiquei com algumas dúvidas:
1.ª - Quando você diz que b = - 4 é porque o gráfico corta o eixo y no sentido descendente? É que substituindo o a = - 2 na equação - b^2 = 8a, fica b^2= 16, Logo, b = +4 ou -4
2.ª - A segunda dúvida é mais grave

tentei resolver o "gráfico B", mas não consegui. O "gráfico C" nem tentei porque o problema que eu tenho é o mesmo, ou seja, como não sei o valor de "c" fico com 3 incógnitas. Explicando o que consegui descobrir do "gráfico B":
a > 0
b < 0
b^2 - 4ac < 0
yv = 1 Logo, 1=(-b^2+4ac)/4a =»
4a = - b^2 + 4acxv = 2 Logo, 2 = - b /2a =»
-b = 4aAgora não consigo sair daqui. Precisava da sua ajuda de novo, se não for pedir muito.
Obrigado
Ricardo
Substituindo: 4a = 16a^2 + 4ac =» 1 = 4a+ c =»
c= 1 - 4a
-
Ricardogferreira
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Jan 23, 2012 21:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Dom Jul 29, 2012 15:14
por DanielFerreira » Dom Jul 29, 2012 15:14
Ricardogferreira escreveu:Obrigado Daniel,
Desculpe incomodar novamente. Compreendi a sua explicação, mas fiquei com algumas dúvidas:
Não há incômodo algum!
Ricardogferreira escreveu:1.ª - Quando você diz que b = - 4 é porque o gráfico corta o eixo y no sentido descendente? É que substituindo o a = - 2 na equação - b^2 = 8a, fica b^2= 16, Logo, b = +4 ou -4
I:
Se

, a equação será
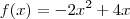
e as raízes

e

. Mas, de acordo com o enunciado...

e
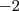
.
II:
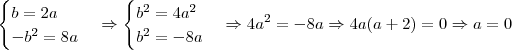
e

Quando

, devemos desconsiderar pois,

. Ou seja, se

a função seria de grau 1!
Quando

:
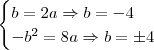 Verificação
Verificação:
Quando

:
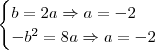
VERDADEIRO
Quando

:

FALSO
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Dom Jul 29, 2012 15:31
por DanielFerreira » Dom Jul 29, 2012 15:31
Ricardogferreira escreveu:...
dados fornecidos no gráfico B (concavidade para cima)- Xv: 2; Yv: 1; GRÁFICO CORTA O EIXO Y EM 3, NO SENTIDO DECRESCENTE - Solução: g(x) = 1/2 (x-2)^2 + 1
...
Ricardo
Ricardogferreira escreveu:...
2.ª - A segunda dúvida é mais grave

tentei resolver o "gráfico B", mas não consegui. O "gráfico C" nem tentei porque o problema que eu tenho é o mesmo, ou seja, como não sei o valor de "c" fico com 3 incógnitas. Explicando o que consegui descobrir do "gráfico B":



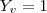
Logo,


Logo,
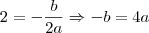 Agora não consigo sair daqui.
Agora não consigo sair daqui. Precisava da sua ajuda de novo, se não for pedir muito.
Obrigado
Ricardo
Faltou vc considerar a condição
SUBLINHADA, ou seja, o ponto
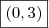
Espero ter ajudado!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Ricardogferreira » Seg Jul 30, 2012 21:28
por Ricardogferreira » Seg Jul 30, 2012 21:28
Apesar de o exercício estar praticamente resolvido, vou então colocar a resolução do "Gráfico B":
a > 0
c = 3
xv = 2 Logo, 2 = - b /2a ==> -b = 4a ==> b = - 4a
yv = 1 Logo, 1 = -

==>
![-\left[{(-4a)}^{2} - 12a\right] -\left[{(-4a)}^{2} - 12a\right]](/latexrender/pictures/3eed2897e0df7f2643405466c060295f.png)
= 4a ==> - (16

- 12a) = 4a ==> -16

+ 8a = 0 ==> a(-16a+8) = 0 ==> a= 0 (Falso: porque a > 0) ou a =

b = -4(

) = - 2
f(x) = a

+ bx + c
f(x) =


- 2x + 3
Convertendo para a forma f(x) = a(x +
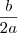
)^2 -

como pretendido nas soluções:
f(x) =

(x-2)^2 + 1
-
Ricardogferreira
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Jan 23, 2012 21:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Seg Jul 30, 2012 21:32
por DanielFerreira » Seg Jul 30, 2012 21:32
Legal!
Vc conseguiu.
E o gráfico

, também conseguiu?
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Ricardogferreira » Seg Jul 30, 2012 21:44
por Ricardogferreira » Seg Jul 30, 2012 21:44
Quanto ao "Gráfico C" voltei a ter problemas porque, desta vez, não sei o Yv...
Estas são as conclusões a que cheguei:
a > 0
b < 0
\Delta > 0
Xv =1 ==> 1 = - b/2a ==> - b = 2a ==> b= - 2a
c = -2
Yv = - (b^2 - 4ac)/4a ==> Yv = - (4a^2 + 8a)/4a ==> Yv = - (a + 2) ==> Yv = -a - 2
A outra conclusão é que ainda tenho muito a aprender ...
-
Ricardogferreira
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Jan 23, 2012 21:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por LuizAquino » Ter Jul 31, 2012 11:58
por LuizAquino » Ter Jul 31, 2012 11:58
Ricardogferreira escreveu:A outra conclusão é que ainda tenho muito a aprender ...
É interessante que você conheça as várias formas de representar uma função polinomial do 2° grau. Cada uma dessas representações será útil em certa situação. As três representações são:
1) forma geral — 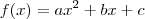
;
2) forma fatorada — 
, onde

e

são as raízes da função;
3) forma canônica (ou padrão) — 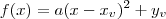
, onde
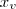
e

são as coordenadas do vértice da parábola.
Qual representação usar irá depender dos dados fornecidos no problema. É óbvio também que você pode passar de uma representação para a outra conforme a necessidade.
No caso do seu exercício, para os gráficos A e B, podemos aplicar diretamente a forma canônica.
Gráfico A — 
,

,

e

.
Desse modo, temos que:
![f(x) = a[x - (-1)]^2 + 2 \implies f(x) = a(x+1)^2 + 2 f(x) = a[x - (-1)]^2 + 2 \implies f(x) = a(x+1)^2 + 2](/latexrender/pictures/128a612332256c5feeea36b6750a6f46.png)
Note que falta apenas determinar o coeficiente a. Para isso, basta usar
qualquer uma das raízes fornecidas. Ou seja, você sabe que acontece f(-2) = 0 e f(0) = 0. Por exemplo, escolhendo f(-2) = 0, temos que:

Portanto, a função para o gráfico A será:

É óbvio que você também poderia ter usado f(0) = 0. No final você chegaria em a = -2 da mesma forma.
Gráfico B — 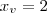
,

, g(0) = 3 (pois o gráfico corta o eixo y em 3).
Tente fazer esse aqui aplicando o mesmo procedimento usado para o A.
Gráfico C — 
,

e h(0) = -2 (pois o gráfico corta o eixo y em -2).
Aqui é mais interessante começar usando a forma fatorada:
 \implies h(x) = a(x + 1)(x - 3) h(x) = a[x - (-1)](x - 3) \implies h(x) = a(x + 1)(x - 3)](/latexrender/pictures/8f518bc5da51e4fbe62a8e873ccb6bb7.png)
Lembrando que h(0) = -2, temos que:
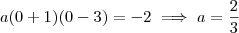
Sendo assim, a função tem o formato fatorado:
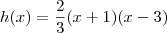
Apesar desta resposta estar correta, desejamos agora colocá-la no formato do gabarito. Afinal de contas, se o exercício fosse de múltipla escolha, deveríamos marcar a opção que corresponde a esta função.
Para transformar a função no formato fatorado para o formado canônico, vamos começar aplicando a distributiva:
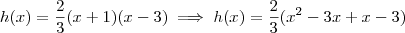
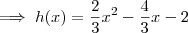
Agora vamos calcular
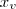
e

:
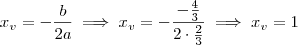
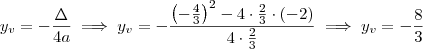
Sendo assim, essa função no formato canônico será:
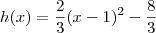
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Ricardogferreira » Ter Jul 31, 2012 20:25
por Ricardogferreira » Ter Jul 31, 2012 20:25
Bom,
Para fechar o tópico e como agradecimento a todos, resta-me então resolver o gráfico B) na forma canónica:

= 2

= 1
g(0) = 3
g(x) = a
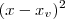
+

g(x) = a
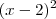
+ 1
3 = a

+ 1

3 = 4a + 1

a =

g(x) =

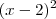
+ 1
Cumprimentos a todos,
Ricardo
-
Ricardogferreira
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Jan 23, 2012 21:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Expressão Álgebrica
por Daniel Gurgel » Ter Set 29, 2009 15:27
- 1 Respostas
- 2227 Exibições
- Última mensagem por DanielFerreira

Qua Set 30, 2009 09:24
Álgebra Elementar
-
- expressão algébrica
por Gustavo R » Sáb Out 08, 2011 16:33
- 1 Respostas
- 1995 Exibições
- Última mensagem por LuizAquino

Dom Out 09, 2011 09:03
Álgebra Elementar
-
- expressão algébrica
por 1000ton » Dom Nov 06, 2011 14:17
- 2 Respostas
- 3588 Exibições
- Última mensagem por Neperiano

Sex Nov 11, 2011 16:23
Álgebra Elementar
-
- expressão algébrica
por Andreza » Qui Jan 19, 2012 11:30
- 1 Respostas
- 1785 Exibições
- Última mensagem por Arkanus Darondra

Qui Jan 19, 2012 12:31
Funções
-
- [Expressão Algébrica]
por Sasuke » Ter Set 02, 2014 10:16
- 1 Respostas
- 1358 Exibições
- Última mensagem por Sasuke

Ter Set 02, 2014 10:33
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.







 e
e 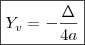

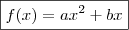

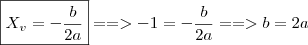

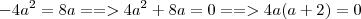
 temos
temos  , com isso,
, com isso, 
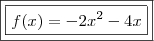


 tentei resolver o "gráfico B", mas não consegui. O "gráfico C" nem tentei porque o problema que eu tenho é o mesmo, ou seja, como não sei o valor de "c" fico com 3 incógnitas. Explicando o que consegui descobrir do "gráfico B":
tentei resolver o "gráfico B", mas não consegui. O "gráfico C" nem tentei porque o problema que eu tenho é o mesmo, ou seja, como não sei o valor de "c" fico com 3 incógnitas. Explicando o que consegui descobrir do "gráfico B":
 , a equação será
, a equação será 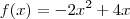 e as raízes
e as raízes  e
e  . Mas, de acordo com o enunciado...
. Mas, de acordo com o enunciado...  e
e 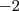 .
.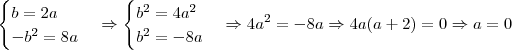 e
e 
 , devemos desconsiderar pois,
, devemos desconsiderar pois,  . Ou seja, se
. Ou seja, se  a função seria de grau 1!
a função seria de grau 1! :
: 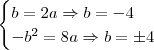
 :
: 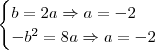 VERDADEIRO
VERDADEIRO :
:  FALSO
FALSO
tentei resolver o "gráfico B", mas não consegui. O "gráfico C" nem tentei porque o problema que eu tenho é o mesmo, ou seja, como não sei o valor de "c" fico com 3 incógnitas. Explicando o que consegui descobrir do "gráfico B":
Logo,
Logo,
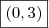

 ==>
==> ![-\left[{(-4a)}^{2} - 12a\right] -\left[{(-4a)}^{2} - 12a\right]](/latexrender/pictures/3eed2897e0df7f2643405466c060295f.png) = 4a ==> - (16
= 4a ==> - (16 - 12a) = 4a ==> -16
- 12a) = 4a ==> -16 + 8a = 0 ==> a(-16a+8) = 0 ==> a= 0 (Falso: porque a > 0) ou a =
+ 8a = 0 ==> a(-16a+8) = 0 ==> a= 0 (Falso: porque a > 0) ou a = 
 ) = - 2
) = - 2 + bx + c
+ bx + c
 - 2x + 3
- 2x + 3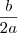 )^2 -
)^2 -  como pretendido nas soluções:
como pretendido nas soluções: (x-2)^2 + 1
(x-2)^2 + 1
 , também conseguiu?
, também conseguiu?

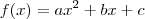 ;
; , onde
, onde  e
e  são as raízes da função;
são as raízes da função;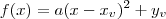 , onde
, onde 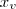 e
e  são as coordenadas do vértice da parábola.
são as coordenadas do vértice da parábola. ,
,  ,
,  e
e  .
.![f(x) = a[x - (-1)]^2 + 2 \implies f(x) = a(x+1)^2 + 2 f(x) = a[x - (-1)]^2 + 2 \implies f(x) = a(x+1)^2 + 2](/latexrender/pictures/128a612332256c5feeea36b6750a6f46.png)


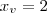 ,
,  , g(0) = 3 (pois o gráfico corta o eixo y em 3).
, g(0) = 3 (pois o gráfico corta o eixo y em 3). ,
,  e h(0) = -2 (pois o gráfico corta o eixo y em -2).
e h(0) = -2 (pois o gráfico corta o eixo y em -2). \implies h(x) = a(x + 1)(x - 3) h(x) = a[x - (-1)](x - 3) \implies h(x) = a(x + 1)(x - 3)](/latexrender/pictures/8f518bc5da51e4fbe62a8e873ccb6bb7.png)
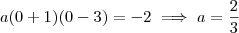
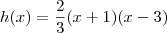
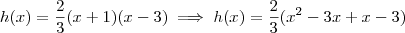
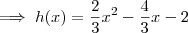
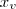 e
e  :
: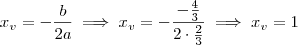
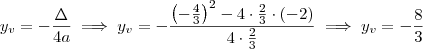
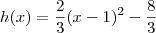

 = 2
= 2 = 1
= 1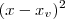 +
+ 
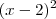 + 1
+ 1 + 1
+ 1  3 = 4a + 1
3 = 4a + 1  a =
a = 

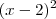 + 1
+ 1
 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: } você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais? } você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?