


 ? existe... existe tg de
? existe... existe tg de  sim existe.
sim existe.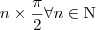
 , pq nao faz sentido calcular a tg... Voce estaria 'dividindo por zero'
, pq nao faz sentido calcular a tg... Voce estaria 'dividindo por zero'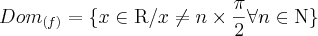
![{Dom}_{(f)}=\{x \in \left[- \pi, \pi \right] / x \neq \frac{\pi}{2} \; , \; \frac{3 \pi}{2}\} {Dom}_{(f)}=\{x \in \left[- \pi, \pi \right] / x \neq \frac{\pi}{2} \; , \; \frac{3 \pi}{2}\}](/latexrender/pictures/767b5530114bcdef760baae2130bd89e.png)




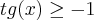
Eu pensei o seguinte: no 1 e 3 quadrante tgx é sempre maior ou igual a -1( pois nesses quadrantes tgx é sempre positiva)
Ja no segundo e quarto quadrante,temos que analisar:se
e
. logo os valores que tornam tgx maiores ou iguais a -1 no segundo e quarto quadrante é
. Logo, o dominio final é:
ou
e
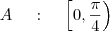
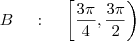
![C \;\;\;\ : \;\;\;\ \left[ \frac{7 \pi}{4} , 2 \pi \right] C \;\;\;\ : \;\;\;\ \left[ \frac{7 \pi}{4} , 2 \pi \right]](/latexrender/pictures/297c022c04a78a4ac1a39c053d73eb9c.png)
![{Dom}_{( tg(x) \geq -1)} = \{ \; x \in \emph{R} \;\; tal \; que \; x \in \left[ 0 , \frac{ \pi}{4} \right) \; ou \; \left[ \frac{3 \pi}{4} , \frac{ 3 \pi}{2} \right) \; ou \; \left[ \frac{7 \pi}{4} , 2 \pi \right] \} {Dom}_{( tg(x) \geq -1)} = \{ \; x \in \emph{R} \;\; tal \; que \; x \in \left[ 0 , \frac{ \pi}{4} \right) \; ou \; \left[ \frac{3 \pi}{4} , \frac{ 3 \pi}{2} \right) \; ou \; \left[ \frac{7 \pi}{4} , 2 \pi \right] \}](/latexrender/pictures/745ce3657553a0566935c384e4762dc3.png)


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)