 por tales » Qui Jul 28, 2011 13:51
por tales » Qui Jul 28, 2011 13:51
Considere a função:
![Z-\left(0 \right)\rightarrow R, f(x)=\sqrt[2]{{3}^{x-2}}\cdot{({9}^{2x+1})}^{\frac{1}{2x}}-{({3}^{2x+5})}^{\frac{1}{x}}+1 Z-\left(0 \right)\rightarrow R, f(x)=\sqrt[2]{{3}^{x-2}}\cdot{({9}^{2x+1})}^{\frac{1}{2x}}-{({3}^{2x+5})}^{\frac{1}{x}}+1](/latexrender/pictures/0ba48cbdc5bbef2734b169c4b026951f.png)
Qual o valor da soma de todos os valores de x para os quais a equação
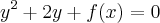
tem raiz dupla ?
Pelo que entendi ele quer a soma das raízes do polinômio:
![p(x)=\sqrt[2]{{3}^{x-2}}\cdot{({9}^{2x+1})}^{\frac{1}{2x}}-{({3}^{2x+5})}^{\frac{1}{x}} p(x)=\sqrt[2]{{3}^{x-2}}\cdot{({9}^{2x+1})}^{\frac{1}{2x}}-{({3}^{2x+5})}^{\frac{1}{x}}](/latexrender/pictures/ea06357a766297da4f09696cd3633ba4.png)
, fiquei uma hora procurando uma forma de encontrá-las, mas não consegui.Se alguém pudesse me ajudar, eu ficaria muito grato.
-
tales
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Jul 28, 2011 10:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: eng. civil
- Andamento: cursando
 por LuizAquino » Qui Jul 28, 2011 16:38
por LuizAquino » Qui Jul 28, 2011 16:38
tales escreveu:Pelo que entendi ele quer a soma das raízes do polinômio:
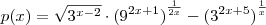
Em primeiro lugar, essa função p não é um "polinômio".
Em segundo, você quer resolver a equação
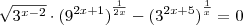
.
Utilizando propriedades de potência, você pode reescrever essa equação como:
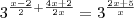
Isso significa que você precisa resolver a equação:
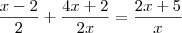
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Fabricio dalla » Qui Jul 28, 2011 17:20
por Fabricio dalla » Qui Jul 28, 2011 17:20
[tex]f(x)=p(x) ?
se for,ta faltando o 1 em p(x)
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Qui Jul 28, 2011 18:23
por LuizAquino » Qui Jul 28, 2011 18:23
Fabricio dalla escreveu:f(x)=p(x) ?
se for,ta faltando o 1 em p(x)
Em nenhum momento foi afirmado que f(x) = p(x).
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Fabricio dalla » Qui Jul 28, 2011 19:37
por Fabricio dalla » Qui Jul 28, 2011 19:37
LuizAquino,quem é p(x) então ?
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Qui Jul 28, 2011 20:32
por LuizAquino » Qui Jul 28, 2011 20:32
Fabricio dalla escreveu:LuizAquino,quem é p(x) então ?
p é uma função que
tales criou na resolução dele.
O que você deve estar querendo saber é
como ele chegou nessa função.
Nesse caso, ele usou o fato de que uma equação polinomial do 2º grau do tipo
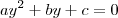
possui raiz dupla quando

, sendo

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por tales » Qui Jul 28, 2011 23:03
por tales » Qui Jul 28, 2011 23:03
Fabricio dalla, meu raciocínio foi o seguinte: para uma equação do 2°grau ter raíz dupla deve posssuir

, nesse caso
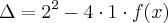
logo
![\sqrt[]{{3}^{x-2}}\cdot{\left({9}^{2x+1} \right)}^{\frac{1}{2x}}-{\left({3}^{2x+5} \right)}^{\frac{1}{x}}=0 \sqrt[]{{3}^{x-2}}\cdot{\left({9}^{2x+1} \right)}^{\frac{1}{2x}}-{\left({3}^{2x+5} \right)}^{\frac{1}{x}}=0](/latexrender/pictures/54c5c77ecb5ef03bfc06766a0cff5ea8.png)
.Para ser mais específico quanto a minha dúvida chamei esta expressão de p(x) e infelizmente compliquei mais.
Editado pela última vez por
tales em Qui Jul 28, 2011 23:04, em um total de 1 vez.
-
tales
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Jul 28, 2011 10:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: eng. civil
- Andamento: cursando
 por tales » Qui Jul 28, 2011 23:03
por tales » Qui Jul 28, 2011 23:03
Muito obrigado pela ajuda.
-
tales
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Jul 28, 2011 10:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: eng. civil
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [P.A.] Exercício
por Cleyson007 » Dom Mai 25, 2008 13:02
- 1 Respostas
- 6557 Exibições
- Última mensagem por admin

Dom Mai 25, 2008 13:20
Progressões
-
- Exercício de PA
por Cleyson007 » Dom Jun 01, 2008 02:45
- 1 Respostas
- 11341 Exibições
- Última mensagem por admin

Dom Jun 01, 2008 14:31
Progressões
-
- Exercício de PA e PG
por Cleyson007 » Sáb Jun 14, 2008 01:21
- 3 Respostas
- 15293 Exibições
- Última mensagem por DanielFerreira

Sex Jul 24, 2009 11:59
Progressões
-
- exercicio de P.G.
por Gir » Qui Jul 02, 2009 18:21
- 3 Respostas
- 4420 Exibições
- Última mensagem por Gir

Sex Jul 03, 2009 10:12
Progressões
-
- exercicio de P.G.
por Gir » Seg Jul 06, 2009 10:54
- 1 Respostas
- 3367 Exibições
- Última mensagem por Marcampucio

Seg Jul 06, 2009 16:33
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![Z-\left(0 \right)\rightarrow R, f(x)=\sqrt[2]{{3}^{x-2}}\cdot{({9}^{2x+1})}^{\frac{1}{2x}}-{({3}^{2x+5})}^{\frac{1}{x}}+1 Z-\left(0 \right)\rightarrow R, f(x)=\sqrt[2]{{3}^{x-2}}\cdot{({9}^{2x+1})}^{\frac{1}{2x}}-{({3}^{2x+5})}^{\frac{1}{x}}+1](/latexrender/pictures/0ba48cbdc5bbef2734b169c4b026951f.png)
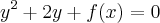 tem raiz dupla ?
tem raiz dupla ?![p(x)=\sqrt[2]{{3}^{x-2}}\cdot{({9}^{2x+1})}^{\frac{1}{2x}}-{({3}^{2x+5})}^{\frac{1}{x}} p(x)=\sqrt[2]{{3}^{x-2}}\cdot{({9}^{2x+1})}^{\frac{1}{2x}}-{({3}^{2x+5})}^{\frac{1}{x}}](/latexrender/pictures/ea06357a766297da4f09696cd3633ba4.png) , fiquei uma hora procurando uma forma de encontrá-las, mas não consegui.Se alguém pudesse me ajudar, eu ficaria muito grato.
, fiquei uma hora procurando uma forma de encontrá-las, mas não consegui.Se alguém pudesse me ajudar, eu ficaria muito grato.

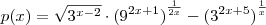
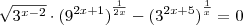 .
.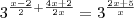
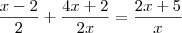


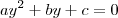 possui raiz dupla quando
possui raiz dupla quando  , sendo
, sendo  .
. , nesse caso
, nesse caso 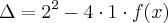 logo
logo ![\sqrt[]{{3}^{x-2}}\cdot{\left({9}^{2x+1} \right)}^{\frac{1}{2x}}-{\left({3}^{2x+5} \right)}^{\frac{1}{x}}=0 \sqrt[]{{3}^{x-2}}\cdot{\left({9}^{2x+1} \right)}^{\frac{1}{2x}}-{\left({3}^{2x+5} \right)}^{\frac{1}{x}}=0](/latexrender/pictures/54c5c77ecb5ef03bfc06766a0cff5ea8.png) .Para ser mais específico quanto a minha dúvida chamei esta expressão de p(x) e infelizmente compliquei mais.
.Para ser mais específico quanto a minha dúvida chamei esta expressão de p(x) e infelizmente compliquei mais.![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.