 por pedro_s_n » Qui Jun 23, 2011 15:41
por pedro_s_n » Qui Jun 23, 2011 15:41
Ola
o problema é o seguinte
fazer o grafico de
f (x) =x³-3x²-9x
calculei a primeira derivada
f '(x) 3x²-6x-9
dps disso nao lembro mais
c alguem puder me dar dicas sobre o que fazer agradeço
obg
-
pedro_s_n
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Jun 23, 2011 15:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por pedro_s_n » Sex Jun 24, 2011 15:39
por pedro_s_n » Sex Jun 24, 2011 15:39
Vi as aulas , me ajudaram mto.
obg
mais ainda estou com duvidas,por exemplo
f(x)=x³-3x²+3
derivo
f '(x)= 3x²-6x
acho o minimo e o maximo reesolvendo a equaçao
x=0,2
estudar o sinal de f(x) e aplicar na parabola.
N~so intendi como se estuda o sinal de uma funçao
-
pedro_s_n
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Jun 23, 2011 15:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por MarceloFantini » Sex Jun 24, 2011 15:49
por MarceloFantini » Sex Jun 24, 2011 15:49
Cuidado quando for escrever, as raízes são

e

. Quando você disse

eu pensei como se fosse o número decimal

. Agora lembre-se: depois de calcular a primeira derivada, verifique onde a função é crescente e decrescente vendo onde ela é positiva e onde ela é negativa. Em seguida, calcule a segunda derivada e ache os pontos de inflexão e onde ela é côncava ou convexa.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por pedro_s_n » Sex Jun 24, 2011 17:34
por pedro_s_n » Sex Jun 24, 2011 17:34
dpois de calcular a primeira derivada, verifique onde a função é crescente e decrescente vendo onde ela é positiva e onde ela é negativa.
por que metodo analiso o sinal da f(x),não intendi pelo material que analisei me pesquisas.
E desculpe pela pressa de escrever,tomarei mais cuidado
sauhsushashau
As raizes achadas podem ser consideradas os pontos criticos da funçao?
-
pedro_s_n
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Jun 23, 2011 15:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por MarceloFantini » Sex Jun 24, 2011 17:59
por MarceloFantini » Sex Jun 24, 2011 17:59
Os pontos onde a derivada é zero são os pontos críticos da função (máximo ou mínimo locais). Agora pegue pontos nos intervalos restantes, e verifique se ela é positiva ou negativa. Um exemplo bem simples, que não é do exercício: vamos supor que a derivada de uma função seja
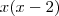
. Os pontos críticos são zero e dois. Agora resta analisar antes de zero, entre zero e dois e depois de dois. Antes de zero, esse produto é positivo, logo a função é positiva e crescente. Entre zero e dois, esse produto é negativo e portanto a função é decrescente(pois x é positivo porém x-2 é negativo). Depois de 2 volta a ser positivo e a função volta a ser crescente.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Gráfico de função trigonométrica-Função seno
 por lucassouza » Dom Mai 31, 2015 19:15
por lucassouza » Dom Mai 31, 2015 19:15
- 0 Respostas
- 1879 Exibições
- Última mensagem por lucassouza

Dom Mai 31, 2015 19:15
Trigonometria
-
- grafico de função
por Amparo » Dom Mar 09, 2008 20:22
- 1 Respostas
- 2566 Exibições
- Última mensagem por admin

Qui Mar 13, 2008 12:56
Funções
-
- Grafico de uma função
por DSR » Qui Ago 27, 2009 21:36
- 3 Respostas
- 2741 Exibições
- Última mensagem por Elcioschin

Sáb Ago 29, 2009 01:05
Álgebra Elementar
-
- Função e gráfico
por rafacosme » Qua Jun 16, 2010 21:31
- 3 Respostas
- 2176 Exibições
- Última mensagem por MarceloFantini

Qui Jun 17, 2010 02:03
Funções
-
- grafico da funçao
 por maria cleide » Qui Mai 12, 2011 17:14
por maria cleide » Qui Mai 12, 2011 17:14
- 1 Respostas
- 1404 Exibições
- Última mensagem por carlosalesouza

Qui Mai 12, 2011 17:23
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






 e
e  . Quando você disse
. Quando você disse  eu pensei como se fosse o número decimal
eu pensei como se fosse o número decimal  . Agora lembre-se: depois de calcular a primeira derivada, verifique onde a função é crescente e decrescente vendo onde ela é positiva e onde ela é negativa. Em seguida, calcule a segunda derivada e ache os pontos de inflexão e onde ela é côncava ou convexa.
. Agora lembre-se: depois de calcular a primeira derivada, verifique onde a função é crescente e decrescente vendo onde ela é positiva e onde ela é negativa. Em seguida, calcule a segunda derivada e ache os pontos de inflexão e onde ela é côncava ou convexa.


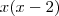 . Os pontos críticos são zero e dois. Agora resta analisar antes de zero, entre zero e dois e depois de dois. Antes de zero, esse produto é positivo, logo a função é positiva e crescente. Entre zero e dois, esse produto é negativo e portanto a função é decrescente(pois x é positivo porém x-2 é negativo). Depois de 2 volta a ser positivo e a função volta a ser crescente.
. Os pontos críticos são zero e dois. Agora resta analisar antes de zero, entre zero e dois e depois de dois. Antes de zero, esse produto é positivo, logo a função é positiva e crescente. Entre zero e dois, esse produto é negativo e portanto a função é decrescente(pois x é positivo porém x-2 é negativo). Depois de 2 volta a ser positivo e a função volta a ser crescente.

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.