 por nietzsche » Ter Jan 24, 2012 22:30
por nietzsche » Ter Jan 24, 2012 22:30
Alguém pode me ajudar?
Sejam T, S operadores lineares de V em V, (V é espaço vetorial). Mostre que se (S o T - I) é injetora entõ (T o S - I) é injetora , (I é a identidade).
(Sugestão: SoT(ToS-I) = (SoT-I)oS.)
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Qua Jan 25, 2012 20:17
por LuizAquino » Qua Jan 25, 2012 20:17
nietzsche escreveu:Sejam T, S operadores lineares de V em V, (V é espaço vetorial). Mostre que se (S o T - I) é injetora entõ (T o S - I) é injetora , (I é a identidade).
(Sugestão: SoT(ToS-I) = (SoT-I)oS.)
Eu presumo que a sugestão na verdade seja
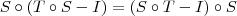
.
Por hipótese,
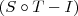
é injetora. Como sabemos que
I é injetora, temos que
S será injetora (justifique essa passagem).
Como
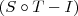
e
S são injetoras, temos que

é injetora (justifique essa passagem).
Lembrando-se das propriedades de composições e que
I é a identidade, podemos escrever que:
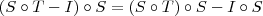
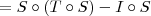
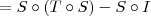
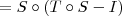
Em resumo, temos que:

Sendo assim, como

é injetora, temos que
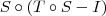
também é injetora.
Como
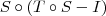
e
S são injetoras, temos que
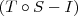
é injetora (justifique essa passagem).
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por nietzsche » Qui Jan 26, 2012 00:27
por nietzsche » Qui Jan 26, 2012 00:27
Olá Luiz,
a dica era a que você falou mesmo, escrevi errado, desculpa.
Você disse:
"Por hipótese, (SoT - I) é injetora. Como sabemos que I é injetora, temos que S será injetora (justifique essa passagem)"
mas como provo que S é injetora?
Acho que o certo é:
Se T é um operador,
ToU = I => T é sobrejetora (no problema não seria S é sobrejtora pois tem inversa a direta?)
SoT = I => T é injetora
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Qui Jan 26, 2012 01:08
por LuizAquino » Qui Jan 26, 2012 01:08
nietzsche escreveu:Você disse:
"Por hipótese, (SoT - I) é injetora. Como sabemos que I é injetora, temos que S será injetora (justifique essa passagem)"
mas como provo que S é injetora?
Que tal pensar mais um pouco sobre o exercício? Eu já indiquei mais de 75% do caminho! Tente continuar!
A ideia é imaginar o que aconteceria com
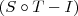
caso
S não fosse injetora.
Comece pelo caso trivial, no qual
S é o operador identicamente nulo.
nietzsche escreveu:Acho que o certo é:
Se T é um operador,
ToU = I => T é sobrejetora (no problema não seria S é sobrejtora pois tem inversa a direta?)
SoT = I => T é injetora
Como
T e
S são de
V em
V, se elas são injetoras, então também são sobrejetoras. O contrário também é válido: se elas são sobrejetoras, então também são injetoras. Use o Teorema do Núcleo e da Imagem para verificar isso.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por nietzsche » Qui Jan 26, 2012 08:28
por nietzsche » Qui Jan 26, 2012 08:28
Mas nesse problema a dimensão do espaço vetorial V não é finita, logo não posso usar o teorema do núcleo/imagem nem dizer que se T é sobrejetiva, então é injetiva.
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Qui Jan 26, 2012 13:54
por LuizAquino » Qui Jan 26, 2012 13:54
nietzsche escreveu:Mas nesse problema a dimensão do espaço vetorial V não é finita, logo não posso usar o teorema do núcleo/imagem nem dizer que se T é sobrejetiva, então é injetiva.
Em que contexto esse exercício foi proposto? Ou seja, que conteúdos foram estudados antes dele? Você retirou esse exercício de algum livro?
Se V for de dimensão infinita, então é necessário mexer mais no caminho que indiquei acima.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por nietzsche » Qui Jan 26, 2012 17:32
por nietzsche » Qui Jan 26, 2012 17:32
Obrigado por responder. Então, o contexto é dum curso de álgebra linear para mestrado, ou um segundo curso de álgebra linear para graduação. Nenhuma hipóstese além das que estão no enunciado podem ser usadas.
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por nietzsche » Qui Jan 26, 2012 17:34
por nietzsche » Qui Jan 26, 2012 17:34
Se quiser tentar resolver, seria bom, mas acabei resolvendo.
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Qui Jan 26, 2012 18:25
por LuizAquino » Qui Jan 26, 2012 18:25
nietzsche escreveu:Se quiser tentar resolver, seria bom, mas acabei resolvendo.
Já que você resolveu, então por favor poste a sua resolução.
Dessa forma, esse tópico ficará completo para futuras referências.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por nietzsche » Qui Jan 26, 2012 20:33
por nietzsche » Qui Jan 26, 2012 20:33
Queremos provar que:
Para todo v

Nuc(ToS-I) => v=0.
Para todo v

Nuc(ToS-I), temos pela definição de núcleo que (ToS-I)(v) = 0. (*)
Aplicando S dos dois lados e usando que S é uma transformação linear: S(ToS-I)(v) = S(0) = 0.
Usando a dica, temos que: (SoT-I)oS(v)=0.
Por hipótese, se SoT-I é injetiva, então Nuc(SoT) = {0}.
Portanto, Sv=0.
Usando que Sv=0 em (*): (ToS-I)(v) = (ToS)(v) -Iv = T(S(v)) - v = T(0)- v =0.
Usando que T é linear: v = T(0) = 0.
Portanto, v=0.
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Qui Jan 26, 2012 21:16
por LuizAquino » Qui Jan 26, 2012 21:16
nietzsche escreveu:Queremos provar que:
Para todo v

Nuc(ToS-I) => v=0.
Para todo v

Nuc(ToS-I), temos pela definição de núcleo que (ToS-I)(v) = 0. (*)
Aplicando S dos dois lados e usando que S é uma transformação linear: S(ToS-I)(v) = S(0) = 0.
Usando a dica, temos que: (SoT-I)oS(v)=0.
Por hipótese, se SoT-I é injetiva, então Nuc(SoT) = {0}.
Portanto, Sv=0.
Usando que Sv=0 em (*): (ToS-I)(v) = (ToS)(v) -Iv = T(S(v)) - v = T(0)- v =0.
Usando que T é linear: v = T(0) = 0.
Portanto, v=0.
Boa solução. Ela serve tanto para V com dimensão finita ou infinita.
Apenas há um erro de digitação na passagem "(...) se SoT-I é injetiva, então Nuc(SoT) = {0}". Na verdade, a última parte seria "então Nuc(SoT-I) = {0}".
Aproveito para fazer uma observação sobre o caminho que indiquei. Eu escrevi acima que:
"(...)
Por hipótese,
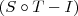
é injetora. Como sabemos que
I é injetora, temos que
S será injetora.
(...)"
Caso
S seja o operador identicamente nulo, temos que
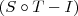
é injetora mesmo sendo
S não injetora.
Entretanto, mesmo nesse caso, temos que
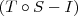
é injetora.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por nietzsche » Qui Jan 26, 2012 23:24
por nietzsche » Qui Jan 26, 2012 23:24
É verdade, tem um erro de digitação. Porém tentei editar o post mas não consegui. Mas obrigado por avisar.
Então, se S é idenicamente nula, vale. Mas se fizer como você disse, assumir que S é injetora, T seria injetora, I injetora, então a composição, soma, etc, também seria injetora e a parte que restaria é provar essas passagens. Valeu pela discussão, achei bem proveitosa.
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Algebra Linear] - Matriz de uma trasnformacao linear, Ajuda
por rodrigojuara » Dom Nov 30, 2014 15:05
- 1 Respostas
- 8159 Exibições
- Última mensagem por adauto martins

Seg Dez 01, 2014 16:12
Álgebra Linear
-
- [Algebra Linear] - Composição de transformação Linear
por aligames321 » Ter Dez 04, 2012 23:53
- 1 Respostas
- 10533 Exibições
- Última mensagem por young_jedi

Qua Dez 05, 2012 12:45
Álgebra Linear
-
- Álgebra Linear -Transformação linear- Isomorfismo
por anapaulasql » Ter Jan 27, 2015 22:08
- 1 Respostas
- 11566 Exibições
- Última mensagem por adauto martins

Ter Mar 29, 2016 13:15
Álgebra Linear
-
- [Álgebra Linear] Transformação Linear Idenpotente
por Zubumafu67 » Ter Nov 17, 2020 11:38
- 0 Respostas
- 13607 Exibições
- Última mensagem por Zubumafu67

Ter Nov 17, 2020 11:38
Álgebra Linear
-
- [Álgebra Linear] Transformação linear
por Debby » Dom Mai 27, 2012 12:17
- 2 Respostas
- 9149 Exibições
- Última mensagem por Debby

Dom Mai 27, 2012 20:27
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



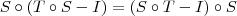 .
.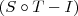 é injetora. Como sabemos que I é injetora, temos que S será injetora (justifique essa passagem).
é injetora. Como sabemos que I é injetora, temos que S será injetora (justifique essa passagem).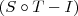 e S são injetoras, temos que
e S são injetoras, temos que  é injetora (justifique essa passagem).
é injetora (justifique essa passagem).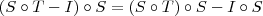
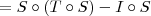
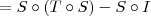
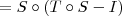

 é injetora, temos que
é injetora, temos que 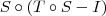 também é injetora.
também é injetora.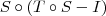 e S são injetoras, temos que
e S são injetoras, temos que 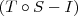 é injetora (justifique essa passagem).
é injetora (justifique essa passagem).

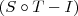 caso S não fosse injetora.
caso S não fosse injetora.





 Nuc(ToS-I) => v=0.
Nuc(ToS-I) => v=0. Nuc(ToS-I), temos pela definição de núcleo que (ToS-I)(v) = 0. (*)
Nuc(ToS-I), temos pela definição de núcleo que (ToS-I)(v) = 0. (*)
Nuc(ToS-I) => v=0.
Nuc(ToS-I), temos pela definição de núcleo que (ToS-I)(v) = 0. (*)
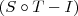 é injetora. Como sabemos que I é injetora, temos que S será injetora.
é injetora. Como sabemos que I é injetora, temos que S será injetora.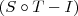 é injetora mesmo sendo S não injetora.
é injetora mesmo sendo S não injetora.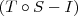 é injetora.
é injetora.

