 por Pessoa Estranha » Qui Nov 13, 2014 22:31
por Pessoa Estranha » Qui Nov 13, 2014 22:31
Olá, pessoal!
Resolvi um exercício e gostaria de saber se está certo.
"Mostre que
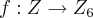
,

é um homomorfismo de grupos."
Minha resolução:
Temos que:
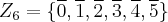
. Observemos que os grupos com os quais estamos trabalhando são

e
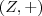
. Vamos mostrar que é homomorfismo. Segue:

;
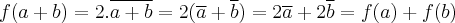
. Conseguimos, assim, mostrar que
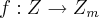
é homomorfismo. Por outro lado, basta observarmos que

pode ser escrito como elemento de
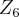
. Por exemplo:

. Logo,
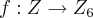
é homomorfismo.
Está certo? Muito obrigada pela ajuda!
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por adauto martins » Qui Nov 20, 2014 14:36
por adauto martins » Qui Nov 20, 2014 14:36
correto,e isso mesmo...sendo

,somente a a propriedade f(x+y)=f(x)+f(y) com x,y inteiros, e verificada...f tambem tem q. ser bijetiva,o q. e facil verificar ai...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Pessoa Estranha » Sex Nov 21, 2014 14:29
por Pessoa Estranha » Sex Nov 21, 2014 14:29
Olá! Muito obrigada pela ajuda!
Só fiquei com uma dúvida: há necessidade mesmo de mostrar que é bijetiva?
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Pessoa Estranha » Sex Nov 21, 2014 14:32
por Pessoa Estranha » Sex Nov 21, 2014 14:32
Depois, o exercício pergunta a Imagem da f. Coloquei assim:
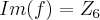
. Está certo?
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por adauto martins » Sex Nov 21, 2014 16:58
por adauto martins » Sex Nov 21, 2014 16:58
nao...me desculpe confundi homomorfismo com isomorfismo... f tem q. ser funçao...qdo funçao bijetiva e homomorfca,entao isomorfica...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Estruturas Algébricas] Homomorfismo
por Pessoa Estranha » Sáb Nov 22, 2014 14:47
- 5 Respostas
- 2557 Exibições
- Última mensagem por adauto martins

Dom Nov 23, 2014 19:53
Álgebra Elementar
-
- Estruturas algébricas
por Eliane Maria » Qua Abr 25, 2012 01:01
- 12 Respostas
- 9140 Exibições
- Última mensagem por fraol

Ter Mai 01, 2012 23:42
Álgebra Elementar
-
- Anéis ( Estruturas algébricas)
por Crist » Qui Mar 20, 2014 15:32
- 1 Respostas
- 2887 Exibições
- Última mensagem por adauto martins

Seg Mar 14, 2016 19:47
Teoria dos Números
-
- [Estruturas algébricas] Anéis
por Crist » Sáb Mar 22, 2014 16:45
- 1 Respostas
- 2085 Exibições
- Última mensagem por adauto martins

Ter Jan 13, 2015 15:45
Álgebra Elementar
-
- [Estruturas Algébricas] Relações
por Pessoa Estranha » Ter Abr 29, 2014 18:28
- 1 Respostas
- 1790 Exibições
- Última mensagem por adauto martins

Sex Dez 05, 2014 17:53
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
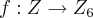 ,
,  é um homomorfismo de grupos."
é um homomorfismo de grupos."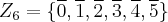 . Observemos que os grupos com os quais estamos trabalhando são
. Observemos que os grupos com os quais estamos trabalhando são  e
e 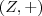 . Vamos mostrar que é homomorfismo. Segue:
. Vamos mostrar que é homomorfismo. Segue:  ;
; 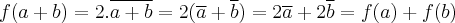 . Conseguimos, assim, mostrar que
. Conseguimos, assim, mostrar que 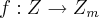 é homomorfismo. Por outro lado, basta observarmos que
é homomorfismo. Por outro lado, basta observarmos que  pode ser escrito como elemento de
pode ser escrito como elemento de 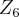 . Por exemplo:
. Por exemplo:  . Logo,
. Logo, 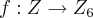 é homomorfismo.
é homomorfismo.

 ,somente a a propriedade f(x+y)=f(x)+f(y) com x,y inteiros, e verificada...f tambem tem q. ser bijetiva,o q. e facil verificar ai...
,somente a a propriedade f(x+y)=f(x)+f(y) com x,y inteiros, e verificada...f tambem tem q. ser bijetiva,o q. e facil verificar ai...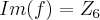 . Está certo?
. Está certo?