Resolvi um exercício e gostaria de saber se está certo.
"Mostre que
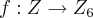 ,
,  é um homomorfismo de grupos."
é um homomorfismo de grupos."Minha resolução:
Temos que:
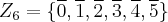 . Observemos que os grupos com os quais estamos trabalhando são
. Observemos que os grupos com os quais estamos trabalhando são  e
e 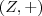 . Vamos mostrar que é homomorfismo. Segue:
. Vamos mostrar que é homomorfismo. Segue:  ;
; 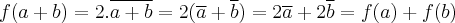 . Conseguimos, assim, mostrar que
. Conseguimos, assim, mostrar que 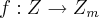 é homomorfismo. Por outro lado, basta observarmos que
é homomorfismo. Por outro lado, basta observarmos que  pode ser escrito como elemento de
pode ser escrito como elemento de 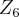 . Por exemplo:
. Por exemplo:  . Logo,
. Logo, 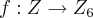 é homomorfismo.
é homomorfismo.Está certo? Muito obrigada pela ajuda!


 ,somente a a propriedade f(x+y)=f(x)+f(y) com x,y inteiros, e verificada...f tambem tem q. ser bijetiva,o q. e facil verificar ai...
,somente a a propriedade f(x+y)=f(x)+f(y) com x,y inteiros, e verificada...f tambem tem q. ser bijetiva,o q. e facil verificar ai...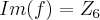 . Está certo?
. Está certo? em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.