 por thadeu » Qua Nov 25, 2009 16:17
por thadeu » Qua Nov 25, 2009 16:17
Qual o maior valor possível de

, onde

são soluções inteiras da equação:
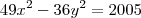
a) 62
b) -4
c) 85
d) -27
-
thadeu
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Out 19, 2009 14:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Adriano Tavares » Ter Mar 08, 2011 22:08
por Adriano Tavares » Ter Mar 08, 2011 22:08
Olá, thadeu.
Como temos um diferença de quadrado podemos escrever essa equação de outra maneira.

Temos então duas possibilidades:
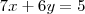


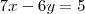
Resolvendo ambos os sistemas encontraremos

e

Portanto,

-
Adriano Tavares
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Seg Mar 07, 2011 16:03
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnólogo em automação industrial
- Andamento: formado
 por Abelardo » Qua Mar 09, 2011 15:38
por Abelardo » Qua Mar 09, 2011 15:38
De onde veio o 5401?
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Abelardo » Qua Mar 09, 2011 22:01
por Abelardo » Qua Mar 09, 2011 22:01
Como você fez isso..
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por LuizAquino » Qua Mar 09, 2011 22:14
por LuizAquino » Qua Mar 09, 2011 22:14
Abelardo escreveu:De onde veio o 5401?
Onde há 5.401 leia
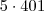
.
Aproveito para deixar uma dica a todos: sempre que precisarem escrever o "ponto central" que representa a multiplicação, usem o comando LaTeX:
- Código: Selecionar todos
[tex]\cdot[/tex]
Por exemplo, para termos
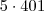
nós digitamos:
- Código: Selecionar todos
[tex]5\cdot 401[/tex]
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Maior valor da inequação
por maria cleide » Dom Mai 29, 2011 17:35
- 8 Respostas
- 4580 Exibições
- Última mensagem por maria cleide

Dom Jun 05, 2011 18:25
Sistemas de Equações
-
- Questão prova concurso (maior valor de y)
por fernandocez » Dom Mar 06, 2011 12:34
- 6 Respostas
- 2998 Exibições
- Última mensagem por LuizAquino

Dom Mar 06, 2011 17:10
Geometria Analítica
-
- Qual é o menor e o maior valor de x na expressão
por andersontricordiano » Seg Out 03, 2011 16:56
- 1 Respostas
- 3939 Exibições
- Última mensagem por MarceloFantini

Seg Out 03, 2011 21:10
Trigonometria
-
- Quem é maior?
por victoreis1 » Qui Nov 25, 2010 18:40
- 19 Respostas
- 16671 Exibições
- Última mensagem por MarceloFantini

Seg Dez 13, 2010 01:24
Desafios Fáceis
-
- maior fator primo
por Marcos Ivan » Sáb Ago 21, 2010 12:29
- 1 Respostas
- 2398 Exibições
- Última mensagem por alexandre32100

Sex Set 24, 2010 17:28
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , onde
, onde  são soluções inteiras da equação:
são soluções inteiras da equação: 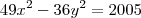

 , onde
, onde  são soluções inteiras da equação:
são soluções inteiras da equação: 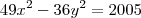


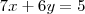


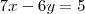
 e
e 




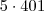 .
.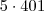 nós digitamos:
nós digitamos:

 .
.



