 por rbhorvath » Qua Nov 21, 2012 15:02
por rbhorvath » Qua Nov 21, 2012 15:02
Olá Pessoal, estou precisando muito da ajuda de vocês pois preciso resolver esse exercício porém não sei absolutamente nada, e se eu não fizer corro o risco de pegar DP na faculdade...
Prove que, para todo n inteiro positivo, é verdadeira a soma:
1^2+3^2+?+(2n-1)^n=n(2n-1)(2n+1)/3
OBS: O pedaço n(2n-1)(2n+1) é inteiro dividido por 3 (Não consegui formatar) e nao somente o (2n+1)
Se alguém puder me ajudar ficarei eternamente grato !
Obrigado !
-
rbhorvath
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qua Nov 21, 2012 14:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: TI
- Andamento: cursando
 por young_jedi » Qua Nov 21, 2012 17:06
por young_jedi » Qua Nov 21, 2012 17:06
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por rbhorvath » Qua Nov 21, 2012 18:27
por rbhorvath » Qua Nov 21, 2012 18:27
young_jedi, MUITO OBRIGADO me ajudou DEMAIS... cara, sou tão ruim que até quando o exercício ta resolvido tenho dificuldade haha

A resposta então seria: 3.(1² + 3² + 5² + 7²....(2n-1)² ?
MUITO OBRIGADO!

-
rbhorvath
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qua Nov 21, 2012 14:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: TI
- Andamento: cursando
 por young_jedi » Qua Nov 21, 2012 18:35
por young_jedi » Qua Nov 21, 2012 18:35
é na ultima equação voce passa o 3 dividindo para o outro lado da expressão e ai voce chega justamente na relação que voce queria demonstrar.
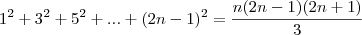
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por rbhorvath » Qua Nov 21, 2012 18:39
por rbhorvath » Qua Nov 21, 2012 18:39
young_jedi escreveu:é na ultima equação voce passa o 3 dividindo para o outro lado da expressão e ai voce chega justamente na relação que voce queria demonstrar.
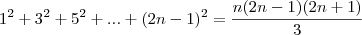
Ok, cara MUITO OBRIGADO por ceder um pouco do seu tempo pra me ajudar obrigado mesmo.
Abraços
-
rbhorvath
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qua Nov 21, 2012 14:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: TI
- Andamento: cursando
 por MarceloFantini » Qua Nov 21, 2012 23:05
por MarceloFantini » Qua Nov 21, 2012 23:05
Apesar de ser uma solução, ela não é por indução.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por rbhorvath » Qua Nov 21, 2012 23:12
por rbhorvath » Qua Nov 21, 2012 23:12
MarceloFantini escreveu:Apesar de ser uma solução, ela não é por indução.
Marcelo, no momento só possuo essa solução que o nosso amigo young_jedi gentilmente resolveu para mim... se você quiser postar outra eu agradeço também !

-
rbhorvath
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qua Nov 21, 2012 14:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: TI
- Andamento: cursando
 por MarceloFantini » Qua Nov 21, 2012 23:26
por MarceloFantini » Qua Nov 21, 2012 23:26
Antes que eu me esqueça, não crie tópicos repetidos. Eu joguei o outro na lixeira.
Resolvi comentar que a solução não é por indução porque, apesar de não ter sido explícito no enunciado, você nomeou o tópico como Indução Matemática. Assim presumi que a idéia é resolver por indução. Você sabe quais são os passos para provar uma afirmação por indução?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por rbhorvath » Qua Nov 21, 2012 23:31
por rbhorvath » Qua Nov 21, 2012 23:31
MarceloFantini escreveu:Antes que eu me esqueça, não crie tópicos repetidos. Eu joguei o outro na lixeira.
Resolvi comentar que a solução não é por indução porque, apesar de não ter sido explícito no enunciado, você nomeou o tópico como Indução Matemática. Assim presumi que a idéia é resolver por indução. Você sabe quais são os passos para provar uma afirmação por indução?
Então estamos aprendendo indução matemática porém no enunciado o professor não especificou o método que deveria ser resolvido portanto acho que não tem importância como é resolvido e sim o resultado...
Não sei como resolver esse exercício por indução matemática
-
rbhorvath
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qua Nov 21, 2012 14:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: TI
- Andamento: cursando
 por MarceloFantini » Qua Nov 21, 2012 23:36
por MarceloFantini » Qua Nov 21, 2012 23:36
rbhorvath escreveu:Então estamos aprendendo indução matemática porém no enunciado o professor não especificou o método que deveria ser resolvido portanto acho que não tem importância como é resolvido e sim o resultado...
Não sei como resolver esse exercício por indução matemática
O resultado você já sabe, não são necessárias todas essas contas. A grande vantagem de demonstrações por indução é justamente provar resultados que não necessariamente tem uma dedução direta.
Para provar um resultado por indução, faça o seguinte:
1) Calcule os dois lados da expressão
separadamente e mostre que são iguais.
2) Assuma que a proposição é válida para

.
3) Mostre que o resultado é válido para

.
Tente fazer o primeiro passo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Cleyson007 » Qui Nov 22, 2012 10:09
por Cleyson007 » Qui Nov 22, 2012 10:09
Olá, bom dia a todos!
Resolvendo por indução:
Vamos provar que a igualdade é válida para n = 1---> 1² = 1(2 - 1)(2 + 1)/3 <---> 1=1 (OK)
Vamos supor que seja válida para n = k ---> 1² + 3² + ... + (2k - 1)² = k(2k - 1)(2k + 1)/3
Logo, também será válida para n = k+1. Acompanhe:
1² + 3² + ... + (2k - 1)² + (2k + 1)² = k(2k - 1)(2k + 1)/3 + 4k² + 4k + 1 = (4n³ + 12n² + 11n + 3)/3 = (k + 1)(2(k + 1) - 1)(2(k + 1) + 1)/3
Comente qualquer dúvida

Att,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por rbhorvath » Qui Nov 22, 2012 14:17
por rbhorvath » Qui Nov 22, 2012 14:17
Cleyson007 escreveu:Olá, bom dia a todos!
Resolvendo por indução:
Vamos provar que a igualdade é válida para n = 1---> 1² = 1(2 - 1)(2 + 1)/3 <---> 1=1 (OK)
Vamos supor que seja válida para n = k ---> 1² + 3² + ... + (2k - 1)² = k(2k - 1)(2k + 1)/3
Logo, também será válida para n = k+1. Acompanhe:
1² + 3² + ... + (2k - 1)² + (2k + 1)² = k(2k - 1)(2k + 1)/3 + 4k² + 4k + 1 = (4n³ + 12n² + 11n + 3)/3 = (k + 1)(2(k + 1) - 1)(2(k + 1) + 1)/3
Comente qualquer dúvida

Att,
Cleyson007
Olá Cleyson, muito obrigado por postar essa solução... posso copiar exatamente do jeito que você postou que estará certo?
-
rbhorvath
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qua Nov 21, 2012 14:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: TI
- Andamento: cursando
 por Cleyson007 » Qui Nov 22, 2012 15:11
por Cleyson007 » Qui Nov 22, 2012 15:11
Olá rbhorvath!
Sim, está correto

Abraço,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por rbhorvath » Sex Nov 23, 2012 16:53
por rbhorvath » Sex Nov 23, 2012 16:53
Cleyson007 escreveu:Olá rbhorvath!
Sim, está correto

Abraço,
Cleyson007
Ok, MUITO OBRIGADO levarei pra faculdade hoje... espero que dê tudo certo !

-
rbhorvath
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qua Nov 21, 2012 14:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: TI
- Andamento: cursando
 por M_Junior » Sáb Abr 05, 2014 22:12
por M_Junior » Sáb Abr 05, 2014 22:12
olá
Estou com dificulades em provar pelo metodo de indução este somátório.

Atenção, que o valor que esta dentro de ( ) não é uma fração.
Será que alguem me pode ajudar.
Obrigado
M_Junior
-
M_Junior
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Abr 05, 2014 21:24
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- induçao matematica ajuda
por xpanhol » Ter Out 18, 2011 15:07
- 3 Respostas
- 2136 Exibições
- Última mensagem por LuizAquino

Qua Out 19, 2011 20:41
Álgebra Elementar
-
- [Provas por Indução Matemática] Ajuda, por favor!
por aprendizdematematico » Seg Abr 30, 2012 14:23
- 1 Respostas
- 1764 Exibições
- Última mensagem por MarceloFantini

Sáb Mai 05, 2012 20:56
Estatística
-
- [hipótese da indução] Indução matemática
por leonardoandra » Sáb Out 12, 2013 22:58
- 1 Respostas
- 2680 Exibições
- Última mensagem por leonardoandra

Seg Out 14, 2013 20:10
Equações
-
- Indução Matemática
por gramata » Qua Set 02, 2009 16:52
- 0 Respostas
- 3063 Exibições
- Última mensagem por gramata

Qua Set 02, 2009 16:52
Problemas do Cotidiano
-
- Indução Matemática
por Abelardo » Qui Mar 31, 2011 03:04
- 1 Respostas
- 2529 Exibições
- Última mensagem por LuizAquino

Qui Mar 31, 2011 11:27
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




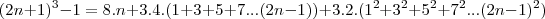



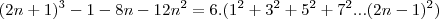
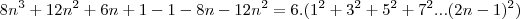
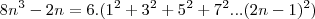
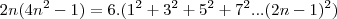
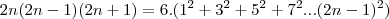





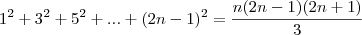









 .
. .
.













 .
.



