Tenho que demonstrar se a afirmação a baixo é verdadeira ou não
![0 < a < b \Rightarrow \sqrt[]{a} < \sqrt[]{b} 0 < a < b \Rightarrow \sqrt[]{a} < \sqrt[]{b}](/latexrender/pictures/a08da913f9d95264dd0e0d81e6c935bc.png)
Obrigado.

![0 < a < b \Rightarrow \sqrt[]{a} < \sqrt[]{b} 0 < a < b \Rightarrow \sqrt[]{a} < \sqrt[]{b}](/latexrender/pictures/a08da913f9d95264dd0e0d81e6c935bc.png)


![\sqrt[]{4} < \sqrt[]{9} \sqrt[]{4} < \sqrt[]{9}](/latexrender/pictures/86fa0cb8f595eb52a00f8f7c2f69af53.png)


Well escreveu:Bem,estou tendo um problema com a demonstração matemática, ainda estou aprendendo.
Tenho que demonstrar se a afirmação a baixo é verdadeira ou não
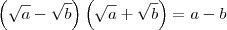 , com a e b números reais positivos.
, com a e b números reais positivos.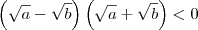
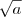 e
e 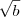 são números positivos (pela definição de raiz quadrada), temos que
são números positivos (pela definição de raiz quadrada), temos que  é um número positivo.
é um número positivo. não é zero. Podemos então dividir toda a inequação anterior por essa soma. Note que a inequação não mudará o seu sentido, pois
não é zero. Podemos então dividir toda a inequação anterior por essa soma. Note que a inequação não mudará o seu sentido, pois  é um número positivo. Temos então que:
é um número positivo. Temos então que:


ednaldo1982 escreveu:0 < 4 < 9

Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.