Verificar se a série é Absolutamente Convergente ou Condicionalmente Convergente

está ok.. temos aqui uma série geométrica

 portanto, divergente...
portanto, divergente...cálculo do módulo:
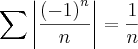 <1, portanto convergente??
<1, portanto convergente??As informações que eu tenho:
-módulo da série sendo convergente= série Absolutamente Convergente
-módulo da série sendo divergente + série
 convergente então = Condicionalmente convergente
convergente então = Condicionalmente convergentesurgiu o questionamento: e se o módulo da série for divergente e a série também?
minha resolução está correta?


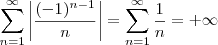 .
.



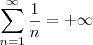 , o que significa que ela é
, o que significa que ela é 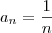 é uma série geométrica, por favor exiba um único número
é uma série geométrica, por favor exiba um único número  tal que
tal que 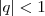 e que
e que 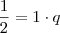 ,
, 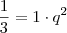 ,
, 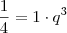 , em diante.
, em diante.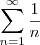 é divergente, como já dito na mensagem anterior e nesta.
é divergente, como já dito na mensagem anterior e nesta.![\sum_{n=1}^{\infty}{\left(\frac{1}{\sqrt[2]{2}} \right)}^{n-1} \sum_{n=1}^{\infty}{\left(\frac{1}{\sqrt[2]{2}} \right)}^{n-1}](/latexrender/pictures/d92ab5170b8a743ac65c72e0d1e69531.png) ???
???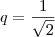 . A sequência é
. A sequência é  , em diante.
, em diante.
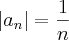 bom.. série harmônica.. p=1 divergente
bom.. série harmônica.. p=1 divergente
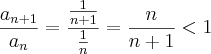
![\left|{a}_{n} \right|=\left|{\left(\frac{1}{\sqrt[]{2}} \right)}^{n-1} \right|=\frac{1}{\sqrt[]{2}}<1\; \left|{a}_{n} \right|=\left|{\left(\frac{1}{\sqrt[]{2}} \right)}^{n-1} \right|=\frac{1}{\sqrt[]{2}}<1\;](/latexrender/pictures/5e01ccedd196df12d16af2aee6faafdf.png)

 , e deve perceber que
, e deve perceber que 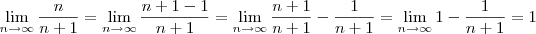 ,
, tende para zero e é monotonamente decrescente, então a série é convergente. Isto é claramente verdade pra série harmônica alternada, então ela converge.
tende para zero e é monotonamente decrescente, então a série é convergente. Isto é claramente verdade pra série harmônica alternada, então ela converge.
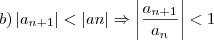
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.