 por Eliane Maria » Qua Abr 25, 2012 01:01
por Eliane Maria » Qua Abr 25, 2012 01:01
Eu preciso verificar se o conjunto dos reais positivos com a operação abaixo representa um grupo.
![x*y = \sqrt[]{x^2+y^2} x*y = \sqrt[]{x^2+y^2}](/latexrender/pictures/c5f35b87f5430258fb09d289bd48c0a7.png)
Eu preciso verificar três propriedades:
1) associatividade - foi verificada
2) existência de elemento neutro - foi verificada. O elemento neutro encontrado foi e =0.
3) existência de elemento simétrico. A minha dúvida é justamente nessa propriedade, pois preciso verificar se
x*x`= e = x`*x, onde x`é o elemento simétrico e "e" o elemento neutro encontrado anteriormente. O desenvolvimento ficou da seguinte forma:
![\sqrt[]{x^2+(x`)^2}=0 \sqrt[]{x^2+(x`)^2}=0](/latexrender/pictures/9f16c6f54261d23cd0de239a33044e6e.png)
. Elevando-se ambos os lados ao quadrado encontramos

. Isolando o x` (elemento simétrico) temos:
![x`= \sqrt[]{-x^2} x`= \sqrt[]{-x^2}](/latexrender/pictures/fa48bfd5fd55e186c919a1a37a33fd2d.png)
.
dúvida: posso extrair a raiz de um número negativo considerando o conjunto dos números reais positivos?
Essa questão está no livro álgebra moderna (Hygino Domingues).
-
Eliane Maria
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Abr 24, 2012 02:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por fraol » Qui Abr 26, 2012 23:49
por fraol » Qui Abr 26, 2012 23:49
Você não pode ter raiz quadrada de número negativo nesse domínio.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Eliane Maria » Sex Abr 27, 2012 12:28
por Eliane Maria » Sex Abr 27, 2012 12:28
Obrigada pela resposta. Foi o que eu pensei também. No livro do Hygino, diz que existe elemento simétrico.
-
Eliane Maria
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Abr 24, 2012 02:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por fraol » Sex Abr 27, 2012 12:55
por fraol » Sex Abr 27, 2012 12:55
Você poderia passar a página do livro que você encontrou o exercício, eu terei acesso ao livro no fim de semana e posso verificar.
No meu entendimento um conjunto munido com essa operação,
![x*y = \sqrt[]{x^2+y^2} x*y = \sqrt[]{x^2+y^2}](/latexrender/pictures/c5f35b87f5430258fb09d289bd48c0a7.png)
, não é um grupo pois não possui o elemento inverso.
Presumo que seja o caso da operação ser algo como
![x*y = \sqrt[2k+1]{x^{2k+1}+y^{2k+1}} x*y = \sqrt[2k+1]{x^{2k+1}+y^{2k+1}}](/latexrender/pictures/bec6d03b2746dee3633d7794d5007578.png)
, isto é o índice e os expoentes devem ser ímpares para poder satisfazer a propriedade do elemento inverso.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Eliane Maria » Seg Abr 30, 2012 00:51
por Eliane Maria » Seg Abr 30, 2012 00:51
Na página 114, no exercício 105, ele pede para o leitor verificar se a operação é associativa. Resp. na página 352. é associativa.
Na página 116, no exercício 111, ele pede para verificar se a operação do exercício 105 tem elemento neutro. Resp. na página 352. tem elemento neutro.
Na página 119, no exercício 116, ele pede para o leitor determinar nas operações do exercício 105 que têm elemento neutro os elementos simetrizavéis. Resp. 352.
Você pode verificar se é isso mesmo?
Mais uma vez obrigada pela ajuda.
Eliane.
-
Eliane Maria
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Abr 24, 2012 02:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por fraol » Seg Abr 30, 2012 20:39
por fraol » Seg Abr 30, 2012 20:39
Boa noite Eliane,
Verifiquei no livro, nesse último exercício, o 116, ele pede os elementos simetrizáveis.
Para o caso que estamos discutindo, somente o

é simetrizável para

.
De fato, o
único elemento que satisfaz a igualdade
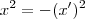
é o

.
Portanto o conjunto

com a operação definida não é um grupo.
Grato.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Eliane Maria » Seg Abr 30, 2012 21:16
por Eliane Maria » Seg Abr 30, 2012 21:16
Olá Fraol,
desculpe, mas eu não entendi.
-
Eliane Maria
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Abr 24, 2012 02:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por fraol » Seg Abr 30, 2012 21:32
por fraol » Seg Abr 30, 2012 21:32
Este exercício pede para você determinar os elementos simetrizáveis dos conjuntos dados.
No caso que estamos discutindo, o da letra c, somente o

é simetrizável, os demais elementos não possuem simétricos pois você cairia naquela impossibilidade da raiz real de número negativo.
Em contraponto, na letra d:

e
![x*y = \sqrt[3]{x^3 + y^3} x*y = \sqrt[3]{x^3 + y^3}](/latexrender/pictures/b606ce34c521a3f6ddfdfb019fe64676.png)
,
todos os elementos são simetrizáveis.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Eliane Maria » Ter Mai 01, 2012 22:07
por Eliane Maria » Ter Mai 01, 2012 22:07
Olá Fraol,
muito obrigada pelo esclarecimento. Se fosse verificada a extração da raiz então posso afirmar que todos os elementos são simetrizáveis? logo a estrutura é um grupo?
-
Eliane Maria
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Abr 24, 2012 02:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por fraol » Ter Mai 01, 2012 22:19
por fraol » Ter Mai 01, 2012 22:19
Eliane Maria escreveu:Olá Fraol,
muito obrigada pelo esclarecimento. Se fosse verificada a extração da raiz então posso afirmar que todos os elementos são simetrizáveis? logo a estrutura é um grupo?
Sim. Se
todos os elementos do conjunto forem
simetrizáveis, existir o
elemento neutro e a
operação for associativa então a estrutura é um grupo.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Eliane Maria » Ter Mai 01, 2012 22:48
por Eliane Maria » Ter Mai 01, 2012 22:48
mais uma vez obrigada. Vou tentar fazer os outros exercícios.
-
Eliane Maria
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Abr 24, 2012 02:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por Eliane Maria » Ter Mai 01, 2012 22:57
por Eliane Maria » Ter Mai 01, 2012 22:57
Fraol,
onde se aplica a teoria dos grupos?
-
Eliane Maria
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Abr 24, 2012 02:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por fraol » Ter Mai 01, 2012 23:42
por fraol » Ter Mai 01, 2012 23:42
Oi
Eliane Maria,
É possível que aqui no forum tenhamos colegas mais preparados para responder essa pergunta.
No entanto, o que posso dizer é que, como muitas partes da matemática, essa teoria servia, inicialmente, a própria matemática.
Mas como ocorre, também com outros tópicos, as aplicações vão surgindo e hoje já há um bom leque delas.
Aqui tem um exemplo prático. Outros exemplos você poderá encontrar na física, na química, na computação, em jogos ( lembra daquele cubo mágico - há formas de resolvê-lo usando teoria dos grupos - um pouco sobre isso você encontra
aqui), etc.
No próprio livro que você está estudando os autores tocam em aplicações na introdução do capítulo IV a respeito desse assunto.
Bons estudos!
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Anéis ( Estruturas algébricas)
por Crist » Qui Mar 20, 2014 15:32
- 1 Respostas
- 2885 Exibições
- Última mensagem por adauto martins

Seg Mar 14, 2016 19:47
Teoria dos Números
-
- [Estruturas algébricas] Anéis
por Crist » Sáb Mar 22, 2014 16:45
- 1 Respostas
- 2084 Exibições
- Última mensagem por adauto martins

Ter Jan 13, 2015 15:45
Álgebra Elementar
-
- [Estruturas Algébricas] Relações
por Pessoa Estranha » Ter Abr 29, 2014 18:28
- 1 Respostas
- 1790 Exibições
- Última mensagem por adauto martins

Sex Dez 05, 2014 17:53
Álgebra Elementar
-
- [Estruturas Algébricas] Funções
por Pessoa Estranha » Sáb Ago 23, 2014 18:01
- 2 Respostas
- 1871 Exibições
- Última mensagem por Pessoa Estranha

Dom Ago 24, 2014 12:29
Álgebra Elementar
-
- [Estruturas Algébricas] Operações
por Pessoa Estranha » Seg Set 15, 2014 17:22
- 2 Respostas
- 3544 Exibições
- Última mensagem por Pessoa Estranha

Ter Set 16, 2014 12:20
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![x*y = \sqrt[]{x^2+y^2} x*y = \sqrt[]{x^2+y^2}](/latexrender/pictures/c5f35b87f5430258fb09d289bd48c0a7.png)
![\sqrt[]{x^2+(x`)^2}=0 \sqrt[]{x^2+(x`)^2}=0](/latexrender/pictures/9f16c6f54261d23cd0de239a33044e6e.png) . Elevando-se ambos os lados ao quadrado encontramos
. Elevando-se ambos os lados ao quadrado encontramos  . Isolando o x` (elemento simétrico) temos:
. Isolando o x` (elemento simétrico) temos: ![x`= \sqrt[]{-x^2} x`= \sqrt[]{-x^2}](/latexrender/pictures/fa48bfd5fd55e186c919a1a37a33fd2d.png) .
. 


![x*y = \sqrt[2k+1]{x^{2k+1}+y^{2k+1}} x*y = \sqrt[2k+1]{x^{2k+1}+y^{2k+1}}](/latexrender/pictures/bec6d03b2746dee3633d7794d5007578.png) , isto é o índice e os expoentes devem ser ímpares para poder satisfazer a propriedade do elemento inverso.
, isto é o índice e os expoentes devem ser ímpares para poder satisfazer a propriedade do elemento inverso. é simetrizável para
é simetrizável para  .
. 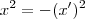 é o
é o  com a operação definida não é um grupo.
com a operação definida não é um grupo. e
e ![x*y = \sqrt[3]{x^3 + y^3} x*y = \sqrt[3]{x^3 + y^3}](/latexrender/pictures/b606ce34c521a3f6ddfdfb019fe64676.png) ,
,