![x*y = \sqrt[]{x^2+y^2} x*y = \sqrt[]{x^2+y^2}](/latexrender/pictures/c5f35b87f5430258fb09d289bd48c0a7.png)
Eu preciso verificar três propriedades:
1) associatividade - foi verificada
2) existência de elemento neutro - foi verificada. O elemento neutro encontrado foi e =0.
3) existência de elemento simétrico. A minha dúvida é justamente nessa propriedade, pois preciso verificar se
x*x`= e = x`*x, onde x`é o elemento simétrico e "e" o elemento neutro encontrado anteriormente. O desenvolvimento ficou da seguinte forma:
![\sqrt[]{x^2+(x`)^2}=0 \sqrt[]{x^2+(x`)^2}=0](/latexrender/pictures/9f16c6f54261d23cd0de239a33044e6e.png) . Elevando-se ambos os lados ao quadrado encontramos
. Elevando-se ambos os lados ao quadrado encontramos  . Isolando o x` (elemento simétrico) temos:
. Isolando o x` (elemento simétrico) temos: ![x`= \sqrt[]{-x^2} x`= \sqrt[]{-x^2}](/latexrender/pictures/fa48bfd5fd55e186c919a1a37a33fd2d.png) .
. dúvida: posso extrair a raiz de um número negativo considerando o conjunto dos números reais positivos?
Essa questão está no livro álgebra moderna (Hygino Domingues).



![x*y = \sqrt[2k+1]{x^{2k+1}+y^{2k+1}} x*y = \sqrt[2k+1]{x^{2k+1}+y^{2k+1}}](/latexrender/pictures/bec6d03b2746dee3633d7794d5007578.png) , isto é o índice e os expoentes devem ser ímpares para poder satisfazer a propriedade do elemento inverso.
, isto é o índice e os expoentes devem ser ímpares para poder satisfazer a propriedade do elemento inverso. é simetrizável para
é simetrizável para  .
. 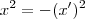 é o
é o  com a operação definida não é um grupo.
com a operação definida não é um grupo. e
e ![x*y = \sqrt[3]{x^3 + y^3} x*y = \sqrt[3]{x^3 + y^3}](/latexrender/pictures/b606ce34c521a3f6ddfdfb019fe64676.png) ,
,  .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
