a) Mostre que f(1)=0
b) mostre que
, sabendo que f(10)=1Na a, eu coloquei que x=1 e y=1 (eu posso fazer isso?)
Mas aí chego que f(1) = 2 :\
Não sei como sair daí...
Na b eu não consegui nem sair do enunciado!
Agradeço se puderem me dar uma luz de como começar a resolver!
e 
, pois lembre-se que o enunciado diz que vale para 
e 
. Agora vamos às contas: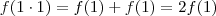
; daí 
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")