 por dimalmeida » Sáb Abr 07, 2012 18:46
por dimalmeida » Sáb Abr 07, 2012 18:46
1) Suponha que f é inversível tal que f(xy)=f(x)+f(y) para todo x e todo y.
a) Mostre que f(1)=0
b) mostre que

, sabendo que f(10)=1
Na a, eu coloquei que x=1 e y=1 (eu posso fazer isso?)
Mas aí chego que f(1) = 2 :\
Não sei como sair daí...
Na b eu não consegui nem sair do enunciado!
Agradeço se puderem me dar uma luz de como começar a resolver!
-
dimalmeida
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Abr 07, 2012 12:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
 por MarceloFantini » Sáb Abr 07, 2012 19:01
por MarceloFantini » Sáb Abr 07, 2012 19:01
Você está fazendo as contas erradas. Você pode sim assumir

e

, pois lembre-se que o enunciado diz que vale para
todo 
e

. Agora vamos às contas:
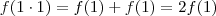
; daí

.
No seu item (b), para escrever elementos superscritos coloque-os entre chaves, como
- Código: Selecionar todos
f^{-1}
Agora, um detalhe: reveja o enunciado, pois falta dizer qual elemento calculamos a inversa.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por dimalmeida » Sáb Abr 07, 2012 19:28
por dimalmeida » Sáb Abr 07, 2012 19:28
O enunciado tá só assim. :/
-
dimalmeida
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Abr 07, 2012 12:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5571 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
-
- [plano tangente a função de duas variaveis dada por função]
por isaac naruto » Qui Dez 31, 2015 16:35
- 0 Respostas
- 4588 Exibições
- Última mensagem por isaac naruto

Qui Dez 31, 2015 16:35
Cálculo: Limites, Derivadas e Integrais
-
- [Desigualdade] entre função exponencial e função potência
por VitorFN » Sex Mai 26, 2017 15:18
- 1 Respostas
- 5741 Exibições
- Última mensagem por adauto martins

Sex Jul 07, 2017 12:17
Álgebra Elementar
-
- +uma função das trevas.ajuda aew!(função par mas heim!?)
por Fabricio dalla » Dom Fev 27, 2011 16:12
- 2 Respostas
- 3484 Exibições
- Última mensagem por LuizAquino

Dom Mar 06, 2011 09:17
Funções
-
- [FUNÇÃO] Não consigo achar a fórmula da função
por LAZAROTTI » Qui Set 27, 2012 00:06
- 1 Respostas
- 2952 Exibições
- Última mensagem por MarceloFantini

Qui Set 27, 2012 07:13
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , sabendo que f(10)=1
, sabendo que f(10)=1

 e
e  , pois lembre-se que o enunciado diz que vale para
, pois lembre-se que o enunciado diz que vale para  e
e  . Agora vamos às contas:
. Agora vamos às contas: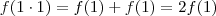 ; daí
; daí  .
.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.