Qual o valor de c?
??c( y² - x² ).(e^(-y)) dx dy = 1 ; -y<x<y ; 0<y< -?
O valor de c é 1/8. Estou com problemas nessa integral gente. Alguma dica?
Muito obrigado.



digsydinner escreveu:Qual o valor de c?
??c( y² - x² ).(e^(-y)) dx dy = 1 ; -y<x<y ; 0<y< -?
O valor de c é 1/8. Estou com problemas nessa integral gente. Alguma dica?


digsydinner escreveu:Amigo eu não sei nem por onde começar. Ja tentei por partes, e substituição. Não saiu em nenhuma das duas...
digsydinner escreveu:Qual o valor de c?
??c( y² - x² ).(e^(-y)) dx dy = 1 ; -y<x<y ; 0<y< -?
 .
.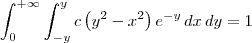
![c\int_{0}^{+\infty}e^{-y}\left[y^2x -\dfrac{1}{3}x^3\right]_{-y}^{y} \, dy = 1 c\int_{0}^{+\infty}e^{-y}\left[y^2x -\dfrac{1}{3}x^3\right]_{-y}^{y} \, dy = 1](/latexrender/pictures/90956b5affcc3bb122738c24770c01ce.png)
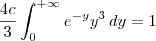

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)