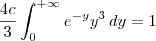por digsydinner » Ter Mar 27, 2012 10:37
por digsydinner » Ter Mar 27, 2012 10:37
Qual o valor de c?
??c( y² - x² ).(e^(-y)) dx dy = 1 ; -y<x<y ; 0<y< -?
O valor de c é 1/8. Estou com problemas nessa integral gente. Alguma dica?
Muito obrigado.
-
digsydinner
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Mar 27, 2012 10:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por LuizAquino » Ter Mar 27, 2012 13:07
por LuizAquino » Ter Mar 27, 2012 13:07
digsydinner escreveu:Qual o valor de c?
??c( y² - x² ).(e^(-y)) dx dy = 1 ; -y<x<y ; 0<y< -?
O valor de c é 1/8. Estou com problemas nessa integral gente. Alguma dica?
Até onde você conseguiu desenvolver? Por favor, mostre a sua tentativa para que possamos corrigi-la.
ObservaçãoPara digitar as notações matemáticas de forma adequada aqui no fórum, por favor leia o tópico:
DICA: Escrevendo Fórmulas com LaTeX via BBCodeviewtopic.php?f=9&t=74
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por digsydinner » Qui Mar 29, 2012 20:50
por digsydinner » Qui Mar 29, 2012 20:50
Amigo eu não sei nem por onde começar. Ja tentei por partes, e substituição. Não saiu em nenhuma das duas...
-
digsydinner
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Mar 27, 2012 10:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por LuizAquino » Sex Mar 30, 2012 00:07
por LuizAquino » Sex Mar 30, 2012 00:07
digsydinner escreveu:Amigo eu não sei nem por onde começar. Ja tentei por partes, e substituição. Não saiu em nenhuma das duas...
Vejamos então o início.
digsydinner escreveu:Qual o valor de c?
??c( y² - x² ).(e^(-y)) dx dy = 1 ; -y<x<y ; 0<y< -?
Eu presumo que o intervalo para y é na verdade

.
Desse modo, temos que:
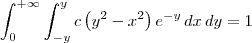
![c\int_{0}^{+\infty}e^{-y}\left[y^2x -\dfrac{1}{3}x^3\right]_{-y}^{y} \, dy = 1 c\int_{0}^{+\infty}e^{-y}\left[y^2x -\dfrac{1}{3}x^3\right]_{-y}^{y} \, dy = 1](/latexrender/pictures/90956b5affcc3bb122738c24770c01ce.png)
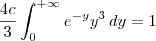
Para resolver essa integral imprópria aplique a integração por partes por três vezes seguidas.
Tente terminar o exercício. Caso continue com dúvidas, coloque aqui até onde você conseguiu desenvolver a partir daí.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Dúvida com uma integral simples
por Leonardo Ribeiro » Sex Abr 03, 2015 20:02
- 1 Respostas
- 2079 Exibições
- Última mensagem por Leonardo Ribeiro

Sex Abr 03, 2015 21:06
Cálculo: Limites, Derivadas e Integrais
-
- [integral] duvida integral
por lucasdemirand » Ter Nov 26, 2013 17:47
- 0 Respostas
- 902 Exibições
- Última mensagem por lucasdemirand

Ter Nov 26, 2013 17:47
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida em Integral
por Cleyson007 » Ter Fev 28, 2012 17:36
- 5 Respostas
- 2184 Exibições
- Última mensagem por LuizAquino

Qui Mar 01, 2012 16:27
Cálculo: Limites, Derivadas e Integrais
-
- Duvida na Integral
por rodrigo ff » Sex Mar 23, 2012 17:44
- 1 Respostas
- 1529 Exibições
- Última mensagem por DanielFerreira

Sex Mar 23, 2012 19:01
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida em Integral
por Cleyson007 » Qua Abr 18, 2012 16:35
- 1 Respostas
- 907 Exibições
- Última mensagem por LuizAquino

Qui Abr 19, 2012 14:36
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 .
.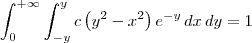
![c\int_{0}^{+\infty}e^{-y}\left[y^2x -\dfrac{1}{3}x^3\right]_{-y}^{y} \, dy = 1 c\int_{0}^{+\infty}e^{-y}\left[y^2x -\dfrac{1}{3}x^3\right]_{-y}^{y} \, dy = 1](/latexrender/pictures/90956b5affcc3bb122738c24770c01ce.png)