Boa tarde pessoal,
estava tentando resolver um exercício de fração com arranjos a questão é a seguinte :
An,2 + An,5 / An,4 esses fatores são iguais a : 9
tentei resolver da seguinte forma
fiz o fatorial de An,2 e An,5 somei e depois anulei com o que estava dividindo mas não chego no número certo, estou perdido pessoal, poderiam me ajudar ?
como devo resolver ? somar todos ou anulr com que esta dividindo ?
Obrigado


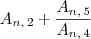
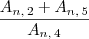


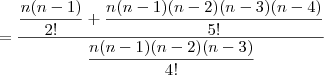

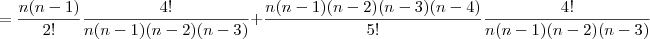
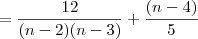



 .
.
 :
: