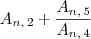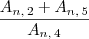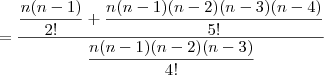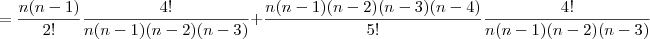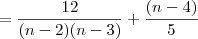por amateurfeet » Dom Mar 11, 2012 16:20
por amateurfeet » Dom Mar 11, 2012 16:20
Boa tarde pessoal,
estava tentando resolver um exercício de fração com arranjos a questão é a seguinte :
An,2 + An,5 / An,4 esses fatores são iguais a : 9
tentei resolver da seguinte forma
fiz o fatorial de An,2 e An,5 somei e depois anulei com o que estava dividindo mas não chego no número certo, estou perdido pessoal, poderiam me ajudar ?
como devo resolver ? somar todos ou anulr com que esta dividindo ?
Obrigado
-
amateurfeet
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Mar 11, 2012 16:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Seg Mar 12, 2012 12:57
por LuizAquino » Seg Mar 12, 2012 12:57
amateurfeet escreveu:estava tentando resolver um exercício de fração com arranjos a questão é a seguinte :
An,2 + An,5 / An,4 esses fatores são iguais a : 9
O que você escreveu é equivalente a:
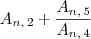
Mas ao que parece, o exercício é:
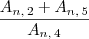
Se esse era o exercício original, então você deveria ter escrito algo como:
(An,2 + An,5)/An,4
Note a importância de usar adequadamente os parênteses!
amateurfeet escreveu:fiz o fatorial de An,2 e An,5 somei e depois anulei com o que estava dividindo mas não chego no número certo, estou perdido pessoal, poderiam me ajudar ?
como devo resolver ? somar todos ou anulr com que esta dividindo ?
Veja o desenvolvimento abaixo.


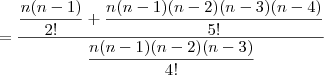

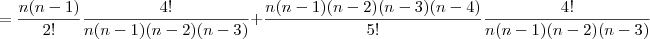
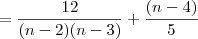

Note que esse desenvolvimento não resulta em 9. O gabarito está errado.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Exercício Frações Equivalentes
por johnlaw » Ter Abr 19, 2011 14:24
- 4 Respostas
- 4289 Exibições
- Última mensagem por johnlaw

Sex Abr 22, 2011 13:28
Álgebra Elementar
-
- [frações] Ajuda pra resolver exercicio
por ERICK12 » Seg Jun 09, 2008 02:41
- 1 Respostas
- 10400 Exibições
- Última mensagem por admin

Seg Jun 09, 2008 15:51
Álgebra Elementar
-
- Arranjos
por scorpion » Dom Out 19, 2008 20:18
- 2 Respostas
- 3577 Exibições
- Última mensagem por scorpion

Seg Out 20, 2008 12:45
Estatística
-
- arranjos simples
por Mi_t » Sex Out 17, 2008 16:25
- 3 Respostas
- 8802 Exibições
- Última mensagem por admin

Qua Out 29, 2008 00:29
Estatística
-
- Combinações vs Arranjos
por joaofonseca » Qua Jan 18, 2012 20:58
- 0 Respostas
- 1043 Exibições
- Última mensagem por joaofonseca

Qua Jan 18, 2012 20:58
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.