 por rodsales » Qui Mai 28, 2009 15:36
por rodsales » Qui Mai 28, 2009 15:36
Estou estudando essa matéria para vestibular e como antes nunca havia estudado, tenho uma dúvida.
Sabemos que o seno de valores notáveis são:
sen 0 = 0
sen

/6 = 1/2
sen

/4 =

/2 e assim sucessivamente.
A dúvida é: Então para sabermos o valor de outros arcos como 2

/3, 3

/4, 5

/6, etc
temos que "decorar" os seus valores através da sua simetria dos arcos notáveis? Existe outra maneira?
Grato,
Aguardo respostas....
-

rodsales
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Ter Abr 14, 2009 21:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: administração
- Andamento: cursando
 por Molina » Qui Mai 28, 2009 19:39
por Molina » Qui Mai 28, 2009 19:39
Boa noite, rodsales.
Desenhe o ciclo trigonométrico primeiramente, marcando os valores que ja sabemos (

,

,

e

). Deixei um modelo em anexo.
Após isso você quer saber quando vale

. Ok, isso é igual a 120° certo?
Só que por identidade trigonométrica, temos que o sen 120° é igual sen 60°
Para verificar isso, localize no ciclo onde fica o 120°. Traçando uma reta pararela ao eixo x, passado pelo 120° você vai ver que no primeiro quadrante, essa reta irá passar pelo 60°.
Ou seja, quando queremos o seno de algum ângulo, queremos saber a distância do ponto que representa esse ângulo no ciclo, até o eixo x. Logo, a distância de 120° até o eixo x é a mesma distância de 60° até o mesmo eixo.
Tente fazer os mesmos ângulos por esse método, ok?
Aguardo por dúvidas.
Bom estudo,

- Anexos
-
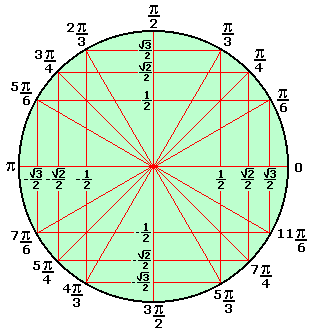
- z_ang.png (3.87 KiB) Exibido 6282 vezes
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por rodsales » Qui Mai 28, 2009 23:17
por rodsales » Qui Mai 28, 2009 23:17
Bem, eu entendi essa parte de passar uma reta até o seno correspodente. Mas, minha dúvida é o seguinte, como que eu sei por exemplo que o ângulo 120°, 2

/3, é equivalemente a 60° ou 225° é equivalente a 315° sem o ciclo trigonométrico? Pois, para montá-lo nesse caso eu teria que decorar todos esses ângulos do ciclo e seus ângulos correspondentes, parece ser meio complicado decorar isso. Por favor me dê uma dica como vc faz.
Grato,
Aguardo respostas.
-

rodsales
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Ter Abr 14, 2009 21:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: administração
- Andamento: cursando
 por Molina » Sex Mai 29, 2009 00:08
por Molina » Sex Mai 29, 2009 00:08
A dica que eu posso dar é você saber construir o ciclo de forma certa e saber os ângulos básicos: 0, 30, 45, 60, 90 e saber utilizar "este recurso" de usar as retas pra passar por primeiro quadrante, sempre tomando cuidado com o sinal, ok?
Conseguiu achar os outros valores que você desconhecia?

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por rodsales » Sex Mai 29, 2009 18:17
por rodsales » Sex Mai 29, 2009 18:17
Opa valeu pelas dicas. Mas farei a última pergunta sobre isso, desculpe por ser insistente, pois realmente preciso aprender isso.
Como exemplo, calcular y:
y = (2 sen 2

/3 - sen

/2)/sen5

/4.
Como vê, o exercício nao apresentou o ciclo trigonométrico, então como que eu saberia que sen5

/4 seria igual a -
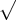
2/2? Bem, eu sei que fica no terceiro quadrante mas no terceiro há mais dois ângulos, 7

/6 e
4
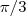
. Entao ai que está a minha dúvida, nesse caso eu teria que decorar os seus valores e seus respectivos ângulos?
210° = -1/2 , 225° = -
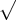
2/2 e 240° = -
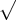
3/2.
Agradeço e desculpe-me pela insistência
Aguardo respostas.
-

rodsales
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Ter Abr 14, 2009 21:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: administração
- Andamento: cursando
 por rodsales » Sex Mai 29, 2009 20:26
por rodsales » Sex Mai 29, 2009 20:26
Molina, agora olhando com mais calma eu entendi.
Obrigado pela ajuda.

-

rodsales
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Ter Abr 14, 2009 21:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: administração
- Andamento: cursando
 por Molina » Sáb Mai 30, 2009 14:59
por Molina » Sáb Mai 30, 2009 14:59
Olá!
Nenhum dos exercícios vai apresentar o ciclo trigonométrico. Isso você mesmo deverá saber montar para resolver as questões sobre trigonometria. Os ângulos básicos que eu disse a cima você também deverá saber. Pelo jeito você está estudando apenas o começo de trigonometria. Virão mais fórmulas, mas para isso você precisa saber já estes sen, cos e tg.
Qualquer dúvida quanto a resolução de algum exercício, basta abrir um novo tópico que alguem vai lhe ajudar. Até mesmo pra voce poder conferir se está fazendo da forma certa.
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Outros sistemas de coordendas
 por Jhenrique » Sex Dez 28, 2012 04:07
por Jhenrique » Sex Dez 28, 2012 04:07
- 1 Respostas
- 1368 Exibições
- Última mensagem por Jhenrique

Seg Dez 31, 2012 23:19
Geometria Analítica
-
- [Matematica Aplicada]-Modulos entre outros.
por Hellsius » Seg Fev 27, 2012 15:30
- 1 Respostas
- 1469 Exibições
- Última mensagem por -Rafael-

Qua Fev 29, 2012 13:19
Sistemas de Equações
-
- [Vetores] Ponto de reta próximo a outros pares de ponto
por cmcrz97 » Ter Jun 19, 2018 20:29
- 0 Respostas
- 2907 Exibições
- Última mensagem por cmcrz97

Ter Jun 19, 2018 20:29
Álgebra Linear
-
- ARCOS
por MERLAYNE » Qua Abr 04, 2012 23:28
- 1 Respostas
- 1544 Exibições
- Última mensagem por MarceloFantini

Qua Abr 04, 2012 23:54
Trigonometria
-
- Arcos - ITA
por DanielFerreira » Dom Abr 29, 2012 21:13
- 1 Respostas
- 1574 Exibições
- Última mensagem por nakagumahissao

Dom Abr 29, 2012 23:28
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 /6 = 1/2
/6 = 1/2 /4 =
/4 =  /2 e assim sucessivamente.
/2 e assim sucessivamente. /3, 3
/3, 3 /4, 5
/4, 5 /6, etc
/6, etc

 ,
,  e
e  ). Deixei um modelo em anexo.
). Deixei um modelo em anexo. . Ok, isso é igual a 120° certo?
. Ok, isso é igual a 120° certo?

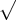 2/2? Bem, eu sei que fica no terceiro quadrante mas no terceiro há mais dois ângulos, 7
2/2? Bem, eu sei que fica no terceiro quadrante mas no terceiro há mais dois ângulos, 7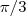 . Entao ai que está a minha dúvida, nesse caso eu teria que decorar os seus valores e seus respectivos ângulos?
. Entao ai que está a minha dúvida, nesse caso eu teria que decorar os seus valores e seus respectivos ângulos?