Boa noite, rodsales.
Desenhe o ciclo trigonométrico primeiramente, marcando os valores que ja sabemos (

,

,

e

). Deixei um modelo em anexo.
Após isso você quer saber quando vale

. Ok, isso é igual a 120° certo?
Só que por identidade trigonométrica, temos que o sen 120° é igual sen 60°
Para verificar isso, localize no ciclo onde fica o 120°. Traçando uma reta pararela ao eixo x, passado pelo 120° você vai ver que no primeiro quadrante, essa reta irá passar pelo 60°.
Ou seja, quando queremos o seno de algum ângulo, queremos saber a distância do ponto que representa esse ângulo no ciclo, até o eixo x. Logo, a distância de 120° até o eixo x é a mesma distância de 60° até o mesmo eixo.
Tente fazer os mesmos ângulos por esse método, ok?
Aguardo por dúvidas.
Bom estudo,

 /6 = 1/2
/6 = 1/2 /4 =
/4 =  /2 e assim sucessivamente.
/2 e assim sucessivamente. /3, 3
/3, 3 /4, 5
/4, 5 /6, etc
/6, etc

 ,
,  e
e  ). Deixei um modelo em anexo.
). Deixei um modelo em anexo. . Ok, isso é igual a 120° certo?
. Ok, isso é igual a 120° certo?

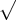 2/2? Bem, eu sei que fica no terceiro quadrante mas no terceiro há mais dois ângulos, 7
2/2? Bem, eu sei que fica no terceiro quadrante mas no terceiro há mais dois ângulos, 7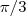 . Entao ai que está a minha dúvida, nesse caso eu teria que decorar os seus valores e seus respectivos ângulos?
. Entao ai que está a minha dúvida, nesse caso eu teria que decorar os seus valores e seus respectivos ângulos?
