[Combinação Linear] com Matrizes, URGENTE!!!

por **cotonete** » Dom Jan 22, 2012 23:34

Olá,
Espero que possam me ajudar estou com dúvida em uma questão onde se pede para determinar o subespaço gerado pelos vetores de um conjunto dado, a questão tem vária letras mas a que me causou duvidas foi a seguinte:

$V = M_2_x_2 (\Re), A = {v_1,v_2,v_3}, onde v_1 = \begin{pmatrix} 2 & -3 \\ 1 & 1 \end{pmatrix} v_2 = \begin{pmatrix} 4 & -6 \\ 2 & 2 \end{pmatrix} v_3 = \begin{pmatrix} 0 & 2 \\ 1 & 0 \end{pmatrix}$

Então eu montei uma equação na qual uma matriz generica 2x2 sera igual a soma dos vetores(v1,v2,v3) multiplicados pelos escalares com os escalares(a,b,c) , com isso chego em um sistema de 4 equações e 3 icógnitas (a,b,c). Só que eu chego no seguinte ponto do sistema e tenho duvida no que fazer:

$\begin{pmatrix} 1 & 2 & 0 & -w \\ 0 & 0 & 0 & y+5w-2z \\ 0 & 0 & 0 & x-2w \\ 0 & 0 & -1 & w-z\\ \end{pmatrix}$

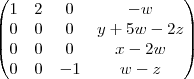
Até pensei em deixar x,y e z em função de w e z e o espaço vetorial seria esse:

$\begin{pmatrix} 2w & 2z-5w \\ z & w \\ \end{pmatrix}$

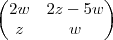
Porém a resposta é essa:

$\begin{pmatrix} 2a & 2b-5a \\ b & a \\ \end{pmatrix}$

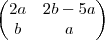
Isso que não entendi, é só chamar w de a e z de b que fica certo,queria saber o que estou errando. Quem souber me ajude pois tenho prova de álgebra linear quinta agora, pois como a faculdade ficou de greve tive apenas 2 semanas de férias. Caso tenha postado no lugar errado me desculpem, sou novo no fórum.

por **MarceloFantini** » Seg Jan 23, 2012 05:52

Mas a letra não faz diferença, sua resposta está certa.

por **cotonete** » Seg Jan 23, 2012 21:50

E eu me matando igual um doido por causa dessas letras,muito obrigado MarceloFantini, pode parecer uma dúvida besta mas eu realmente não estava seguro com aquela respoosta, mas agora percebi que estou pelo caminho certo.