Sn=9+99+999+…+10n -1
Sabendo que se trata da soma dos termos de uma P.G.''
Eu sei sobre o termo geral de uma P.G. e como calcular com a formula do termo geral de uma P.G.(an=a1.
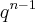
porem não estou conseguindo resolver esta questão, já que não consigo aplicar na formula, agradeço a quem puder me ajudar,
pois semana que vem haverá uma avaliação referente ao assunto e uma lista de exercicio.
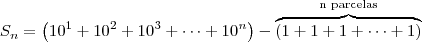
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)