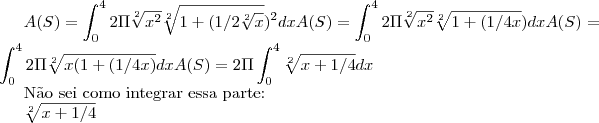
Se alguem puder me ajudar ficaria muito feliz... Obrigada

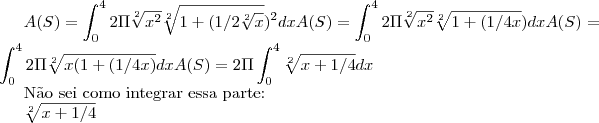

martinay escreveu:
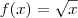 , então a integral correta seria:
, então a integral correta seria: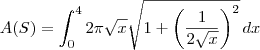
 ao invés de
ao invés de  .
.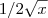 . Mas isso é o mesmo que
. Mas isso é o mesmo que 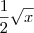 .
. , então aí sim você tem algo equivalente a
, então aí sim você tem algo equivalente a  .
.martinay escreveu:
Não sei como integrar essa parte:
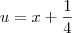 .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: