 por maykonnunes » Seg Set 19, 2011 11:07
por maykonnunes » Seg Set 19, 2011 11:07
Suponha que a quantidade de petróleo bombeada de um poço, diminui a uma taxa contínua de 10% por ano. Quando a produçãao do poço atingirá um quinto de seu valor atual? (Resolva usando EDO)
Estou sem idéia de inicio acho que me falta interpretação
-
maykonnunes
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 02:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por LuizAquino » Seg Set 19, 2011 11:21
por LuizAquino » Seg Set 19, 2011 11:21
maykonnunes escreveu:Suponha que a quantidade de petróleo bombeada de um poço, diminui a uma taxa contínua de 10% por ano. (...)
Seja P(t) a quantidade de petróleo no tempo t. Desse modo, temos que:
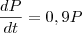
maykonnunes escreveu:(...) Quando a produçãao do poço atingirá um quinto de seu valor atual?
Suponha que

. Você deseja calcular o tempo
t tal que

.
maykonnunes escreveu:Estou sem idéia de inicio acho que me falta interpretação
De fato, interpretação foi o que faltou.

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por maykonnunes » Seg Set 19, 2011 12:45
por maykonnunes » Seg Set 19, 2011 12:45
LuizAquino, de f ( y) y ' = g(x) , usando a forma dy/dx=y´ segue que f ( y)dy = g(x)dx
não estou conseguindo identificar os termos para integrar
se puder dar mais uma mão fico agradecido.
-
maykonnunes
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 02:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por maykonnunes » Ter Set 20, 2011 15:08
por maykonnunes » Ter Set 20, 2011 15:08
Luiz, bom acho que entedi algumas coisas, se eu pensar em uma PG onde primerio termo Po razao 0,9
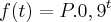
, então P é constante

é a váriavel, mas não consigo colocar está ideia em EDO.
Ou seja a ideia é assim:
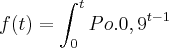
ai basta resolver a integral??
e fazer

??
encontro a solução??
-
maykonnunes
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 02:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por MarceloFantini » Ter Set 20, 2011 18:37
por MarceloFantini » Ter Set 20, 2011 18:37
Não necessariamente é uma progressão geométrica. Resolva a integral e use as informações que o colega Luiz Aquino te indicou.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por maykonnunes » Ter Set 20, 2011 19:33
por maykonnunes » Ter Set 20, 2011 19:33
"LuizAquino disse
Note que:

Bom resolvendo tenho:

proximo passo??
-
maykonnunes
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 02:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por MarceloFantini » Ter Set 20, 2011 19:40
por MarceloFantini » Ter Set 20, 2011 19:40
Não se esqueça da constante.
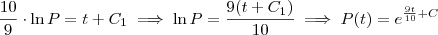
. Lembre-se que

, que é a quantidade inicial. Depois disso, faça

e encontre t.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por maykonnunes » Qua Set 21, 2011 00:13
por maykonnunes » Qua Set 21, 2011 00:13
Segundo meu tutor
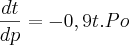
ai fica
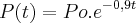
, ai então
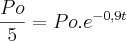
que:
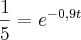
ai daqui para frente não consigo mais solucionar
-
maykonnunes
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 02:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- PA (não sei resolver)
por Bruninha » Qua Mar 04, 2009 19:00
- 2 Respostas
- 5767 Exibições
- Última mensagem por ivolatanza

Sex Mar 06, 2009 23:37
Progressões
-
- Resolver a equação
por thadeu » Dom Nov 22, 2009 23:01
- 0 Respostas
- 835 Exibições
- Última mensagem por thadeu

Dom Nov 22, 2009 23:01
Álgebra Elementar
-
- Como resolver
por thyssa » Ter Abr 19, 2011 22:06
- 1 Respostas
- 2963 Exibições
- Última mensagem por FilipeCaceres

Ter Abr 19, 2011 23:31
Progressões
-
- Como Resolver.
por 380625 » Dom Set 11, 2011 14:36
- 1 Respostas
- 1908 Exibições
- Última mensagem por MarceloFantini

Dom Set 11, 2011 19:40
Matrizes e Determinantes
-
- Como resolver!!
por MW2 » Qui Jan 05, 2012 16:44
- 1 Respostas
- 1945 Exibições
- Última mensagem por Arkanus Darondra

Qui Jan 05, 2012 18:41
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



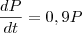
 . Você deseja calcular o tempo t tal que
. Você deseja calcular o tempo t tal que  .
.


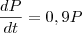
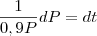


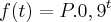 , então P é constante
, então P é constante  é a váriavel, mas não consigo colocar está ideia em EDO.
é a váriavel, mas não consigo colocar está ideia em EDO.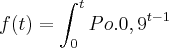
 ??
??





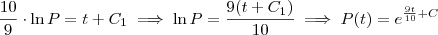 . Lembre-se que
. Lembre-se que  , que é a quantidade inicial. Depois disso, faça
, que é a quantidade inicial. Depois disso, faça  e encontre t.
e encontre t.

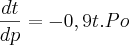 ai fica
ai fica 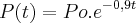 , ai então
, ai então 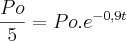 que:
que: 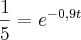 ai daqui para frente não consigo mais solucionar
ai daqui para frente não consigo mais solucionar
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
