 por Flavia R » Qui Ago 25, 2011 12:07
por Flavia R » Qui Ago 25, 2011 12:07
Considerando-se que a equação
![senx.cosx=\frac{\sqrt[2]{3}}{4}} senx.cosx=\frac{\sqrt[2]{3}}{4}}](/latexrender/pictures/9da870b4b0435111d3176814b72155e0.png)
tem n soluções no intervalo
![[0,2\Pi] [0,2\Pi]](/latexrender/pictures/7e326c0277c2130a5a16165614b20484.png)
, pode-se afirmar que o valor de n é:
bom, eu tentei elevar os dois lados ao quadrado já, mas não fechou..
-
Flavia R
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Ago 24, 2011 17:14
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: curso técnico em agrimensura
- Andamento: formado
 por gvm » Qui Ago 25, 2011 21:40
por gvm » Qui Ago 25, 2011 21:40
Bom, uma dica pra resolver esse tipo de exercício, onde você tem

em um dos membros é se lembrar das relações de Arco Duplo, mais especificamente dessa aqui:

Pensa em como utilizar isso no exercício em questão, você vai acabar chegando a uma expressão bem mais simples do que se elevasse os dois membros ao quadrado e utilizasse
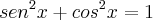
para deixar toda a expressão em função do seno ou cosseno
Espero ter ajudado.
-
gvm
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Ago 25, 2011 00:02
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibulando Engenharia
- Andamento: cursando
 por Flavia R » Qui Ago 25, 2011 22:01
por Flavia R » Qui Ago 25, 2011 22:01
na verdade, eu não consigo ver como a fórmula do arco duplo pode me ajudar..:S
-
Flavia R
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Ago 24, 2011 17:14
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: curso técnico em agrimensura
- Andamento: formado
 por gvm » Qui Ago 25, 2011 22:09
por gvm » Qui Ago 25, 2011 22:09
A expressão é a seguinte:
![senx . cosx = \sqrt[2]{3}/4 senx . cosx = \sqrt[2]{3}/4](/latexrender/pictures/3090ab3e2f3e0be0010e985e3268dcae.png)
Multiplicando os dois membros da equação por 2 obtem-se:
![2.senx . cosx = \sqrt[2]{3}/2 2.senx . cosx = \sqrt[2]{3}/2](/latexrender/pictures/1e1d7db4d9522ac460a941320a32aa98.png)
Sabe-se que
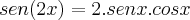
, portanto:
![sen(2x) = \sqrt[2]{3}/2 sen(2x) = \sqrt[2]{3}/2](/latexrender/pictures/888b7f9725fa7bd7660f0fe08d75d73a.png)
Agora que temos toda a expressão em função apenas do seno é só resolver normalmente e encontrar as soluções contidas no intervalo especificado, lembrando que as soluções da equação são os valores de

e não de

.
Esperto ter ajudado
-
gvm
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Ago 25, 2011 00:02
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibulando Engenharia
- Andamento: cursando
Voltar para Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![senx.cosx=\frac{\sqrt[2]{3}}{4}} senx.cosx=\frac{\sqrt[2]{3}}{4}}](/latexrender/pictures/9da870b4b0435111d3176814b72155e0.png) tem n soluções no intervalo
tem n soluções no intervalo ![[0,2\Pi] [0,2\Pi]](/latexrender/pictures/7e326c0277c2130a5a16165614b20484.png) , pode-se afirmar que o valor de n é:
, pode-se afirmar que o valor de n é:
![senx.cosx=\frac{\sqrt[2]{3}}{4}} senx.cosx=\frac{\sqrt[2]{3}}{4}}](/latexrender/pictures/9da870b4b0435111d3176814b72155e0.png) tem n soluções no intervalo
tem n soluções no intervalo ![[0,2\Pi] [0,2\Pi]](/latexrender/pictures/7e326c0277c2130a5a16165614b20484.png) , pode-se afirmar que o valor de n é:
, pode-se afirmar que o valor de n é:
 em um dos membros é se lembrar das relações de Arco Duplo, mais especificamente dessa aqui:
em um dos membros é se lembrar das relações de Arco Duplo, mais especificamente dessa aqui:
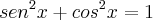 para deixar toda a expressão em função do seno ou cosseno
para deixar toda a expressão em função do seno ou cosseno

![senx . cosx = \sqrt[2]{3}/4 senx . cosx = \sqrt[2]{3}/4](/latexrender/pictures/3090ab3e2f3e0be0010e985e3268dcae.png)
![2.senx . cosx = \sqrt[2]{3}/2 2.senx . cosx = \sqrt[2]{3}/2](/latexrender/pictures/1e1d7db4d9522ac460a941320a32aa98.png)
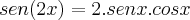 , portanto:
, portanto:![sen(2x) = \sqrt[2]{3}/2 sen(2x) = \sqrt[2]{3}/2](/latexrender/pictures/888b7f9725fa7bd7660f0fe08d75d73a.png)
 e não de
e não de  .
.





