 por Flavia R » Qui Ago 25, 2011 12:07
por Flavia R » Qui Ago 25, 2011 12:07
Considerando-se que a equação
![senx.cosx=\frac{\sqrt[2]{3}}{4}} senx.cosx=\frac{\sqrt[2]{3}}{4}}](/latexrender/pictures/9da870b4b0435111d3176814b72155e0.png)
tem n soluções no intervalo
![[0,2\Pi] [0,2\Pi]](/latexrender/pictures/7e326c0277c2130a5a16165614b20484.png)
, pode-se afirmar que o valor de n é:
bom, eu tentei elevar os dois lados ao quadrado já, mas não fechou..
-
Flavia R
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Ago 24, 2011 17:14
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: curso técnico em agrimensura
- Andamento: formado
 por gvm » Qui Ago 25, 2011 21:40
por gvm » Qui Ago 25, 2011 21:40
Bom, uma dica pra resolver esse tipo de exercício, onde você tem

em um dos membros é se lembrar das relações de Arco Duplo, mais especificamente dessa aqui:

Pensa em como utilizar isso no exercício em questão, você vai acabar chegando a uma expressão bem mais simples do que se elevasse os dois membros ao quadrado e utilizasse
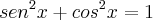
para deixar toda a expressão em função do seno ou cosseno
Espero ter ajudado.
-
gvm
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Ago 25, 2011 00:02
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibulando Engenharia
- Andamento: cursando
 por Flavia R » Qui Ago 25, 2011 22:01
por Flavia R » Qui Ago 25, 2011 22:01
na verdade, eu não consigo ver como a fórmula do arco duplo pode me ajudar..:S
-
Flavia R
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Ago 24, 2011 17:14
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: curso técnico em agrimensura
- Andamento: formado
 por gvm » Qui Ago 25, 2011 22:09
por gvm » Qui Ago 25, 2011 22:09
A expressão é a seguinte:
![senx . cosx = \sqrt[2]{3}/4 senx . cosx = \sqrt[2]{3}/4](/latexrender/pictures/3090ab3e2f3e0be0010e985e3268dcae.png)
Multiplicando os dois membros da equação por 2 obtem-se:
![2.senx . cosx = \sqrt[2]{3}/2 2.senx . cosx = \sqrt[2]{3}/2](/latexrender/pictures/1e1d7db4d9522ac460a941320a32aa98.png)
Sabe-se que
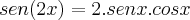
, portanto:
![sen(2x) = \sqrt[2]{3}/2 sen(2x) = \sqrt[2]{3}/2](/latexrender/pictures/888b7f9725fa7bd7660f0fe08d75d73a.png)
Agora que temos toda a expressão em função apenas do seno é só resolver normalmente e encontrar as soluções contidas no intervalo especificado, lembrando que as soluções da equação são os valores de

e não de

.
Esperto ter ajudado
-
gvm
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Ago 25, 2011 00:02
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibulando Engenharia
- Andamento: cursando
Voltar para Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![senx.cosx=\frac{\sqrt[2]{3}}{4}} senx.cosx=\frac{\sqrt[2]{3}}{4}}](/latexrender/pictures/9da870b4b0435111d3176814b72155e0.png) tem n soluções no intervalo
tem n soluções no intervalo ![[0,2\Pi] [0,2\Pi]](/latexrender/pictures/7e326c0277c2130a5a16165614b20484.png) , pode-se afirmar que o valor de n é:
, pode-se afirmar que o valor de n é:
![senx.cosx=\frac{\sqrt[2]{3}}{4}} senx.cosx=\frac{\sqrt[2]{3}}{4}}](/latexrender/pictures/9da870b4b0435111d3176814b72155e0.png) tem n soluções no intervalo
tem n soluções no intervalo ![[0,2\Pi] [0,2\Pi]](/latexrender/pictures/7e326c0277c2130a5a16165614b20484.png) , pode-se afirmar que o valor de n é:
, pode-se afirmar que o valor de n é:
 em um dos membros é se lembrar das relações de Arco Duplo, mais especificamente dessa aqui:
em um dos membros é se lembrar das relações de Arco Duplo, mais especificamente dessa aqui:
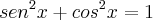 para deixar toda a expressão em função do seno ou cosseno
para deixar toda a expressão em função do seno ou cosseno

![senx . cosx = \sqrt[2]{3}/4 senx . cosx = \sqrt[2]{3}/4](/latexrender/pictures/3090ab3e2f3e0be0010e985e3268dcae.png)
![2.senx . cosx = \sqrt[2]{3}/2 2.senx . cosx = \sqrt[2]{3}/2](/latexrender/pictures/1e1d7db4d9522ac460a941320a32aa98.png)
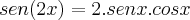 , portanto:
, portanto:![sen(2x) = \sqrt[2]{3}/2 sen(2x) = \sqrt[2]{3}/2](/latexrender/pictures/888b7f9725fa7bd7660f0fe08d75d73a.png)
 e não de
e não de  .
.

 .
.



