


Maykids escreveu:Encontre o valor extato:
a) arccos (cos(2,8))
 , isto te dará um valor A, por exemplo. Agora você precisa calcular o valor de
, isto te dará um valor A, por exemplo. Agora você precisa calcular o valor de  . O que o arccos quer saber qual valor de cosseno dá o valor de A.
. O que o arccos quer saber qual valor de cosseno dá o valor de A. , pois o cosseno de 0 é 1.
, pois o cosseno de 0 é 1.Maykids escreveu:Alguem tem video ou uma boa explicação sobre Funções inversas


 , f(a)=b , f'(a)=m , quando podemos garantir que g'(b) existe? Demonstre como encontrar g'(b).
, f(a)=b , f'(a)=m , quando podemos garantir que g'(b) existe? Demonstre como encontrar g'(b).






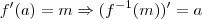


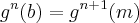

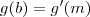 , então é válido que
, então é válido que  .
.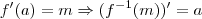
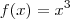 e
e ![g(x) = \sqrt[3]{x} g(x) = \sqrt[3]{x}](/latexrender/pictures/a54c9ebe80f6e252270c9c9e5e7257fb.png) . Naturalmente f e g são funções inversas. Entretanto, note que f'(2) = 12 e g'(12) =
. Naturalmente f e g são funções inversas. Entretanto, note que f'(2) = 12 e g'(12) = ![\frac{\sqrt[3]{12}}{36} \frac{\sqrt[3]{12}}{36}](/latexrender/pictures/f37ed666f59c1a0108a20b760756e8b1.png) .
.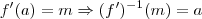 , desde que f' possua inversa.
, desde que f' possua inversa.


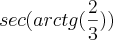
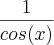


Maykids escreveu:agora há a possibilidade de ser cos(arccos(2.8)) = 2.8 também?
Maykids escreveu:agora vamos deixar a coisa mais animada, rss..:
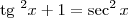 , temos que
, temos que  .
.![\sec\left[\textrm{arctg}\left(\frac{2}{3}\right)\right] = \sqrt{\left\{\textrm{tg }\left[\textrm{arctg}\left(\frac{2}{3}\right)\right] \right\}^2 + 1} \sec\left[\textrm{arctg}\left(\frac{2}{3}\right)\right] = \sqrt{\left\{\textrm{tg }\left[\textrm{arctg}\left(\frac{2}{3}\right)\right] \right\}^2 + 1}](/latexrender/pictures/7088a8d50e46836814ce5f6390e654b2.png) .
.
![\sec\left[\textrm{arctg}\left(\frac{2}{3}\right)\right] = \sqrt{\left\{\textrm{tg }\left[\textrm{arctg}\left(\frac{2}{3}\right)\right] \right\}^2 + 1} \sec\left[\textrm{arctg}\left(\frac{2}{3}\right)\right] = \sqrt{\left\{\textrm{tg }\left[\textrm{arctg}\left(\frac{2}{3}\right)\right] \right\}^2 + 1}](/latexrender/pictures/7088a8d50e46836814ce5f6390e654b2.png)

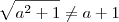 .
.



![\sqrt[]{\frac{4}{9}+1} = \sqrt[]{\frac{13}{9}}
= \frac{\sqrt[]{13}}{3} \sqrt[]{\frac{4}{9}+1} = \sqrt[]{\frac{13}{9}}
= \frac{\sqrt[]{13}}{3}](/latexrender/pictures/1132512debbc981612b234a7d1668076.png)

![\sec\left[\textrm{arctg}\left(\frac{2}{3}\right)\right] = \sqrt{\left\{\textrm{tg }\left[\textrm{arctg}\left(\frac{2}{3}\right)\right] \right\}^2 + 1} = \frac{\sqrt{13}}{3} \sec\left[\textrm{arctg}\left(\frac{2}{3}\right)\right] = \sqrt{\left\{\textrm{tg }\left[\textrm{arctg}\left(\frac{2}{3}\right)\right] \right\}^2 + 1} = \frac{\sqrt{13}}{3}](/latexrender/pictures/8473cfb67d107c34c33d6db74209eaa1.png)


 por
por  , nós obtemos a identidade
, nós obtemos a identidade 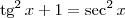 (quando
(quando 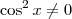 ).
).
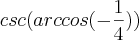


![cosc(x) = \sqrt[]{cotg^(x)+1} cosc(x) = \sqrt[]{cotg^(x)+1}](/latexrender/pictures/495bf653ed02c460164dad93a6d31158.png)

 .
.
![sen(x) = +-\sqrt[]{1-cos^2(x)} sen(x) = +-\sqrt[]{1-cos^2(x)}](/latexrender/pictures/a3ff52aec4bb44b8cc2aa5b56352f413.png)
![cosc(x)= \frac{1}{\sqrt[]{1-cos^2(x)}} cosc(x)= \frac{1}{\sqrt[]{1-cos^2(x)}}](/latexrender/pictures/eefde50b73f4d0e7c8f740277b7ec6f9.png)
![\frac{1}{\sqrt[]{1-cos^2(x)}}(arccos(-\frac{1}{4))} \frac{1}{\sqrt[]{1-cos^2(x)}}(arccos(-\frac{1}{4))}](/latexrender/pictures/bdd740a0a832efd6f87cb29745bde5e9.png)

Maykids escreveu: é que não tive uma base muito forte nessa parte de trigonometria :s
Maykids escreveu:já descobri que sem estudar não dá pra passar...



Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes