Ola, estou a estudar para o exame da segunda fase de mat e preciso de ajuda com alguns exercícios.
Uma caixa contem 2 bolas pretas, uma bola verde e n bolas amarelas. Considere a seguinte experiência: ao acaso, retiram-se simultaneamente duas bolas da caixa.
Sabendo que a probabilidade de uma ser amarela e a outra verde é de 5/39, determine o valor de n.
Eles resolvem o exercício usando esta equação n/(1+n)combinações de 2 = 5/39 e o resultado da 10. Eu não entendo como é que eles chegaram à equação.
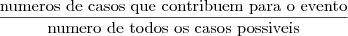
bolas, uma retirada corresponde a uma combinação de duas bolas. Assim, o número de retiradas corresponde ao número de combinações de 
a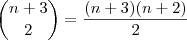 
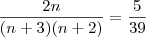que é uma equação do segundo grau em 
, cuja raiz natural é 
, de fato.
por ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.