Estou precisando da ajuda para calcular o limite nessa questão :
![lim_{x\rightarrow0}\frac{\sqrt[3]{x}^{2}-2\sqrt[3]{x}+1}{(x-1)^2} lim_{x\rightarrow0}\frac{\sqrt[3]{x}^{2}-2\sqrt[3]{x}+1}{(x-1)^2}](/latexrender/pictures/7b54080ab6ded82daa58f791f4a9849b.png)
Agradeço desde já!


![lim_{x\rightarrow0}\frac{\sqrt[3]{x}^{2}-2\sqrt[3]{x}+1}{(x-1)^2} lim_{x\rightarrow0}\frac{\sqrt[3]{x}^{2}-2\sqrt[3]{x}+1}{(x-1)^2}](/latexrender/pictures/7b54080ab6ded82daa58f791f4a9849b.png)


![(\sqrt[3]{x} - 1)^2 (\sqrt[3]{x} - 1)^2](/latexrender/pictures/7a25102f7c33b960cb17b39921dd7493.png) .
.  .
.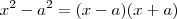 . Podemos obter esta igualdade também pela divisão do polinômio
. Podemos obter esta igualdade também pela divisão do polinômio  por
por  . Trocando
. Trocando  por
por  e
e  por
por 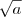 temos
temos 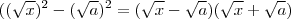 . Observe que o primeiro membro fica
. Observe que o primeiro membro fica  e assim obtem-se a identidade
e assim obtem-se a identidade 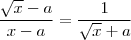 .Evidentemente há formas mais diretas de obter esta identidade ,e.g. , multiplicando em cima e em baixo pelo conjugado de
.Evidentemente há formas mais diretas de obter esta identidade ,e.g. , multiplicando em cima e em baixo pelo conjugado de 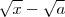 , entretanto este raciocinio falha para o caso
, entretanto este raciocinio falha para o caso ![\sqrt[3]{x} - \sqrt[3]{a} \sqrt[3]{x} - \sqrt[3]{a}](/latexrender/pictures/b880959da811be97867fd03c58e27e25.png) .
. por
por  é
é 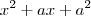 e o resto constante ; logo polinômio nulo ...Assim ,
e o resto constante ; logo polinômio nulo ...Assim , 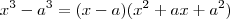 .
.  por
por ![\sqrt[3]{x} \sqrt[3]{x}](/latexrender/pictures/6833f4eaccfb60d5c13fdf6b6cc30aef.png) e
e  por
por ![\sqrt[3]{a} \sqrt[3]{a}](/latexrender/pictures/76b1e479f805bb036a3487aeb35932e5.png) temos
temos ![((\sqrt[3]{x})^3 -(\sqrt[3]{a})^3 = (\sqrt[3]{x} -\sqrt[3]{a})((\sqrt[3]{x} )^2 + (\sqrt[3]{a} (\sqrt[3]{x} + (\sqrt[3]{a} )^2 )) ((\sqrt[3]{x})^3 -(\sqrt[3]{a})^3 = (\sqrt[3]{x} -\sqrt[3]{a})((\sqrt[3]{x} )^2 + (\sqrt[3]{a} (\sqrt[3]{x} + (\sqrt[3]{a} )^2 ))](/latexrender/pictures/2c2d22668782886c290a045df8cc9f10.png) . Observe que o primeiro membro fica
. Observe que o primeiro membro fica  e assim obtem-se a identidade
e assim obtem-se a identidade ![\frac{\sqrt{x} - \srqt{a} }{x-a } = \frac{1}{(\sqrt[3]{x} )^2 + (\sqrt[3]{a} (\sqrt[3]{x} + (\sqrt[3]{a} )^2} \frac{\sqrt{x} - \srqt{a} }{x-a } = \frac{1}{(\sqrt[3]{x} )^2 + (\sqrt[3]{a} (\sqrt[3]{x} + (\sqrt[3]{a} )^2}](/latexrender/pictures/822d79b6f48b8d0146ac910f30c7456b.png)
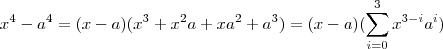
![\frac{ \sqrt[4]{x} - \sqrt[4]{a}}{x-a} = \frac{1}{\sum_{i=0}^{3} (\sqrt[4]{x})^{3-i} (\sqrt[4]{a})^i} \frac{ \sqrt[4]{x} - \sqrt[4]{a}}{x-a} = \frac{1}{\sum_{i=0}^{3} (\sqrt[4]{x})^{3-i} (\sqrt[4]{a})^i}](/latexrender/pictures/41467f7f9695bb79a710a51e5124585a.png)

![\frac{\sqrt[n]{x} - \sqrt[n]{a} }{x-a} = \frac{1}{\sum_{i=0}^{n-1} x^{n-1-i} a^i } \frac{\sqrt[n]{x} - \sqrt[n]{a} }{x-a} = \frac{1}{\sum_{i=0}^{n-1} x^{n-1-i} a^i }](/latexrender/pictures/441b0ee931c473699f94a3ab6071d81c.png)

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.