a)
![\lim_{x\rightarrow2} \frac{\sqrt[2]{x^2+x-2} - \sqrt[2]{x^2-x+2}}{\sqrt[2]{x+2}-2} \lim_{x\rightarrow2} \frac{\sqrt[2]{x^2+x-2} - \sqrt[2]{x^2-x+2}}{\sqrt[2]{x+2}-2}](/latexrender/pictures/840dbdd9e32284955786c043ed401d06.png)
b)
![\lim_{x\rightarrow2} \frac{\sqrt[]{2x^2-3x+2}-2}{\sqrt[]{3x^2-5x-1}-1} \lim_{x\rightarrow2} \frac{\sqrt[]{2x^2-3x+2}-2}{\sqrt[]{3x^2-5x-1}-1}](/latexrender/pictures/af813c95f3a865a0ecce89010f9be08f.png)
c)
![\lim_{x\rightarrow0} \frac{\sqrt[3]{2x^2-3x+2}-2}{x-x^2} \lim_{x\rightarrow0} \frac{\sqrt[3]{2x^2-3x+2}-2}{x-x^2}](/latexrender/pictures/06fc63530f262c21993f50c894ffe7de.png)
d) Calcule a,b

 de forma que
de forma que 
e)
![\lim_{x\rightarrow4} \frac{\sqrt[]{x}-2}{\sqrt[]{x-4}} \lim_{x\rightarrow4} \frac{\sqrt[]{x}-2}{\sqrt[]{x-4}}](/latexrender/pictures/969161c9ddd009c7c49e2013f217a6f6.png)
f)
![\lim_{x\rightarrow1} \frac{\sqrt[]{x+2}-\sqrt[]{3}}{x^3-1} \lim_{x\rightarrow1} \frac{\sqrt[]{x+2}-\sqrt[]{3}}{x^3-1}](/latexrender/pictures/7587bb4de99e48b2cac1c68986c67402.png)
g)
![\lim_{x\rightarrow11} \frac{\sqrt[]{x}- \sqrt[]{11}}{\sqrt[]{x+11}- \sqrt[]{22}} \lim_{x\rightarrow11} \frac{\sqrt[]{x}- \sqrt[]{11}}{\sqrt[]{x+11}- \sqrt[]{22}}](/latexrender/pictures/b5a65e87edf8d556f9d36cd0d6e562d6.png)

![\lim_{x\rightarrow2} \frac{\sqrt[2]{x^2+x-2} - \sqrt[2]{x^2-x+2}}{\sqrt[2]{x+2}-2} \lim_{x\rightarrow2} \frac{\sqrt[2]{x^2+x-2} - \sqrt[2]{x^2-x+2}}{\sqrt[2]{x+2}-2}](/latexrender/pictures/840dbdd9e32284955786c043ed401d06.png)
![\lim_{x\rightarrow2} \frac{\sqrt[]{2x^2-3x+2}-2}{\sqrt[]{3x^2-5x-1}-1} \lim_{x\rightarrow2} \frac{\sqrt[]{2x^2-3x+2}-2}{\sqrt[]{3x^2-5x-1}-1}](/latexrender/pictures/af813c95f3a865a0ecce89010f9be08f.png)
![\lim_{x\rightarrow0} \frac{\sqrt[3]{2x^2-3x+2}-2}{x-x^2} \lim_{x\rightarrow0} \frac{\sqrt[3]{2x^2-3x+2}-2}{x-x^2}](/latexrender/pictures/06fc63530f262c21993f50c894ffe7de.png)

 de forma que
de forma que 
![\lim_{x\rightarrow4} \frac{\sqrt[]{x}-2}{\sqrt[]{x-4}} \lim_{x\rightarrow4} \frac{\sqrt[]{x}-2}{\sqrt[]{x-4}}](/latexrender/pictures/969161c9ddd009c7c49e2013f217a6f6.png)
![\lim_{x\rightarrow1} \frac{\sqrt[]{x+2}-\sqrt[]{3}}{x^3-1} \lim_{x\rightarrow1} \frac{\sqrt[]{x+2}-\sqrt[]{3}}{x^3-1}](/latexrender/pictures/7587bb4de99e48b2cac1c68986c67402.png)
![\lim_{x\rightarrow11} \frac{\sqrt[]{x}- \sqrt[]{11}}{\sqrt[]{x+11}- \sqrt[]{22}} \lim_{x\rightarrow11} \frac{\sqrt[]{x}- \sqrt[]{11}}{\sqrt[]{x+11}- \sqrt[]{22}}](/latexrender/pictures/b5a65e87edf8d556f9d36cd0d6e562d6.png)

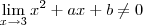 . Neste caso o limite são será indeterminado ,logo podemos usar uma das regras operacionais , a saber , a regra do quociente para obter "(algum número diferente de zero )/(número muito próximo de zero) " , o resultado entre aspas sabemos é que
. Neste caso o limite são será indeterminado ,logo podemos usar uma das regras operacionais , a saber , a regra do quociente para obter "(algum número diferente de zero )/(número muito próximo de zero) " , o resultado entre aspas sabemos é que 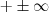 (dependo do sinal do número) .Absurdo ! Logo só podemos ter
(dependo do sinal do número) .Absurdo ! Logo só podemos ter 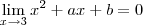 .Logo ,
.Logo , 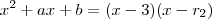 (forma fatorada) [r_2 a segunda raiz do polinômio .
(forma fatorada) [r_2 a segunda raiz do polinômio . 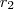 que em consequência obterá as constantes pedidas .
que em consequência obterá as constantes pedidas .
 para que a = -1 e b = -6 e lim = 5.
para que a = -1 e b = -6 e lim = 5.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 12 visitantes

 .
.



