 por baloso » Sex Abr 25, 2014 19:22
por baloso » Sex Abr 25, 2014 19:22
Olá pessoal, tentei resolver esses limites por conjugados e outras propriedades mas não consegui. Alguém pode me falar quais propriedades eu uso? Mt obg
a)
![\lim_{x\rightarrow2} \frac{\sqrt[2]{x^2+x-2} - \sqrt[2]{x^2-x+2}}{\sqrt[2]{x+2}-2} \lim_{x\rightarrow2} \frac{\sqrt[2]{x^2+x-2} - \sqrt[2]{x^2-x+2}}{\sqrt[2]{x+2}-2}](/latexrender/pictures/840dbdd9e32284955786c043ed401d06.png)
b)
![\lim_{x\rightarrow2} \frac{\sqrt[]{2x^2-3x+2}-2}{\sqrt[]{3x^2-5x-1}-1} \lim_{x\rightarrow2} \frac{\sqrt[]{2x^2-3x+2}-2}{\sqrt[]{3x^2-5x-1}-1}](/latexrender/pictures/af813c95f3a865a0ecce89010f9be08f.png)
c)
![\lim_{x\rightarrow0} \frac{\sqrt[3]{2x^2-3x+2}-2}{x-x^2} \lim_{x\rightarrow0} \frac{\sqrt[3]{2x^2-3x+2}-2}{x-x^2}](/latexrender/pictures/06fc63530f262c21993f50c894ffe7de.png)
d) Calcule a,b


de forma que

e)
![\lim_{x\rightarrow4} \frac{\sqrt[]{x}-2}{\sqrt[]{x-4}} \lim_{x\rightarrow4} \frac{\sqrt[]{x}-2}{\sqrt[]{x-4}}](/latexrender/pictures/969161c9ddd009c7c49e2013f217a6f6.png)
f)
![\lim_{x\rightarrow1} \frac{\sqrt[]{x+2}-\sqrt[]{3}}{x^3-1} \lim_{x\rightarrow1} \frac{\sqrt[]{x+2}-\sqrt[]{3}}{x^3-1}](/latexrender/pictures/7587bb4de99e48b2cac1c68986c67402.png)
g)
![\lim_{x\rightarrow11} \frac{\sqrt[]{x}- \sqrt[]{11}}{\sqrt[]{x+11}- \sqrt[]{22}} \lim_{x\rightarrow11} \frac{\sqrt[]{x}- \sqrt[]{11}}{\sqrt[]{x+11}- \sqrt[]{22}}](/latexrender/pictures/b5a65e87edf8d556f9d36cd0d6e562d6.png)
-
baloso
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Abr 25, 2014 18:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por e8group » Sáb Abr 26, 2014 00:36
por e8group » Sáb Abr 26, 2014 00:36
Boa noite . De acordo com as regras da casa , uma questão por tópico .
Vou te dar uma dica item (d) .
Suponha inicialmente
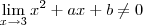
. Neste caso o limite são será indeterminado ,logo podemos usar uma das regras operacionais , a saber , a regra do quociente para obter "(algum número diferente de zero )/(número muito próximo de zero) " , o resultado entre aspas sabemos é que
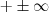
(dependo do sinal do número) .Absurdo ! Logo só podemos ter
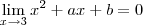
.Logo ,
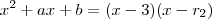
(forma fatorada) [r_2 a segunda raiz do polinômio .
Agora utilizando a forma fatora e a hipótese do limite ser 5 , encontre
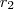
que em consequência obterá as constantes pedidas .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por baloso » Seg Abr 28, 2014 19:33
por baloso » Seg Abr 28, 2014 19:33
Eu entendi o que você quis dizer. Só olhando deu pra identificar que a raiz é 2.
Então temos que usar

para que a = -1 e b = -6 e lim = 5.
Porém eu não faço a mínima ideia de como provar isso... Eu não posso simplesmente falar que a segunda raiz é 2 e pronto né?
-
baloso
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Abr 25, 2014 18:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [raíz quadrada] Dificuldade com raízes quadradas..
por lucas7 » Ter Ago 30, 2011 21:39
- 5 Respostas
- 3096 Exibições
- Última mensagem por lucas7

Qua Ago 31, 2011 15:18
Conversão de Unidades
-
- Dificuldade com limites e módulos
por Luisags » Qui Abr 12, 2012 23:05
- 5 Respostas
- 3831 Exibições
- Última mensagem por gabriel feron

Ter Abr 17, 2012 03:17
Cálculo: Limites, Derivadas e Integrais
-
- Dificuldade com limites em cálculo I
por Vidotti » Dom Nov 04, 2012 20:42
- 4 Respostas
- 2494 Exibições
- Última mensagem por Vidotti

Dom Nov 04, 2012 21:17
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITES] Limites com duas raízes
por Atom » Dom Mai 25, 2014 20:22
- 1 Respostas
- 2059 Exibições
- Última mensagem por e8group

Dom Mai 25, 2014 21:59
Cálculo: Limites, Derivadas e Integrais
-
- Limites, conjugado de raizes
por moyses » Qui Out 06, 2011 12:16
- 19 Respostas
- 25709 Exibições
- Última mensagem por LuizAquino

Dom Out 09, 2011 19:16
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow2} \frac{\sqrt[2]{x^2+x-2} - \sqrt[2]{x^2-x+2}}{\sqrt[2]{x+2}-2} \lim_{x\rightarrow2} \frac{\sqrt[2]{x^2+x-2} - \sqrt[2]{x^2-x+2}}{\sqrt[2]{x+2}-2}](/latexrender/pictures/840dbdd9e32284955786c043ed401d06.png)
![\lim_{x\rightarrow2} \frac{\sqrt[]{2x^2-3x+2}-2}{\sqrt[]{3x^2-5x-1}-1} \lim_{x\rightarrow2} \frac{\sqrt[]{2x^2-3x+2}-2}{\sqrt[]{3x^2-5x-1}-1}](/latexrender/pictures/af813c95f3a865a0ecce89010f9be08f.png)
![\lim_{x\rightarrow0} \frac{\sqrt[3]{2x^2-3x+2}-2}{x-x^2} \lim_{x\rightarrow0} \frac{\sqrt[3]{2x^2-3x+2}-2}{x-x^2}](/latexrender/pictures/06fc63530f262c21993f50c894ffe7de.png)

 de forma que
de forma que 
![\lim_{x\rightarrow4} \frac{\sqrt[]{x}-2}{\sqrt[]{x-4}} \lim_{x\rightarrow4} \frac{\sqrt[]{x}-2}{\sqrt[]{x-4}}](/latexrender/pictures/969161c9ddd009c7c49e2013f217a6f6.png)
![\lim_{x\rightarrow1} \frac{\sqrt[]{x+2}-\sqrt[]{3}}{x^3-1} \lim_{x\rightarrow1} \frac{\sqrt[]{x+2}-\sqrt[]{3}}{x^3-1}](/latexrender/pictures/7587bb4de99e48b2cac1c68986c67402.png)
![\lim_{x\rightarrow11} \frac{\sqrt[]{x}- \sqrt[]{11}}{\sqrt[]{x+11}- \sqrt[]{22}} \lim_{x\rightarrow11} \frac{\sqrt[]{x}- \sqrt[]{11}}{\sqrt[]{x+11}- \sqrt[]{22}}](/latexrender/pictures/b5a65e87edf8d556f9d36cd0d6e562d6.png)

![\lim_{x\rightarrow2} \frac{\sqrt[2]{x^2+x-2} - \sqrt[2]{x^2-x+2}}{\sqrt[2]{x+2}-2} \lim_{x\rightarrow2} \frac{\sqrt[2]{x^2+x-2} - \sqrt[2]{x^2-x+2}}{\sqrt[2]{x+2}-2}](/latexrender/pictures/840dbdd9e32284955786c043ed401d06.png)
![\lim_{x\rightarrow2} \frac{\sqrt[]{2x^2-3x+2}-2}{\sqrt[]{3x^2-5x-1}-1} \lim_{x\rightarrow2} \frac{\sqrt[]{2x^2-3x+2}-2}{\sqrt[]{3x^2-5x-1}-1}](/latexrender/pictures/af813c95f3a865a0ecce89010f9be08f.png)
![\lim_{x\rightarrow0} \frac{\sqrt[3]{2x^2-3x+2}-2}{x-x^2} \lim_{x\rightarrow0} \frac{\sqrt[3]{2x^2-3x+2}-2}{x-x^2}](/latexrender/pictures/06fc63530f262c21993f50c894ffe7de.png)

 de forma que
de forma que 
![\lim_{x\rightarrow4} \frac{\sqrt[]{x}-2}{\sqrt[]{x-4}} \lim_{x\rightarrow4} \frac{\sqrt[]{x}-2}{\sqrt[]{x-4}}](/latexrender/pictures/969161c9ddd009c7c49e2013f217a6f6.png)
![\lim_{x\rightarrow1} \frac{\sqrt[]{x+2}-\sqrt[]{3}}{x^3-1} \lim_{x\rightarrow1} \frac{\sqrt[]{x+2}-\sqrt[]{3}}{x^3-1}](/latexrender/pictures/7587bb4de99e48b2cac1c68986c67402.png)
![\lim_{x\rightarrow11} \frac{\sqrt[]{x}- \sqrt[]{11}}{\sqrt[]{x+11}- \sqrt[]{22}} \lim_{x\rightarrow11} \frac{\sqrt[]{x}- \sqrt[]{11}}{\sqrt[]{x+11}- \sqrt[]{22}}](/latexrender/pictures/b5a65e87edf8d556f9d36cd0d6e562d6.png)

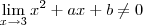 . Neste caso o limite são será indeterminado ,logo podemos usar uma das regras operacionais , a saber , a regra do quociente para obter "(algum número diferente de zero )/(número muito próximo de zero) " , o resultado entre aspas sabemos é que
. Neste caso o limite são será indeterminado ,logo podemos usar uma das regras operacionais , a saber , a regra do quociente para obter "(algum número diferente de zero )/(número muito próximo de zero) " , o resultado entre aspas sabemos é que 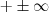 (dependo do sinal do número) .Absurdo ! Logo só podemos ter
(dependo do sinal do número) .Absurdo ! Logo só podemos ter 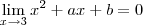 .Logo ,
.Logo , 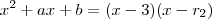 (forma fatorada) [r_2 a segunda raiz do polinômio .
(forma fatorada) [r_2 a segunda raiz do polinômio . 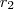 que em consequência obterá as constantes pedidas .
que em consequência obterá as constantes pedidas .
 para que a = -1 e b = -6 e lim = 5.
para que a = -1 e b = -6 e lim = 5.