 por Razoli » Qua Jan 08, 2014 16:25
por Razoli » Qua Jan 08, 2014 16:25
Olá, tenho uma dúvida referente:
O QUE É esse CORPO "K" , onde o conjunto V esta sobre o mesmo, não estou entendendo o que é esse corpo! Alguém poderia me explicar de forma bastante intuitiva?
-
Razoli
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sáb Abr 06, 2013 15:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatistica
- Andamento: cursando
 por anderson_wallace » Qua Jan 08, 2014 18:21
por anderson_wallace » Qua Jan 08, 2014 18:21
Um corpo numérico é um subconjunto
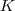
de números complexos (note que o conjunto dos reais também está contido em K) que é fechado em relação as operações elementares, ou seja, se vc somar, subtrair,multiplicar ou dividir (com divisor diferente de 0) elementos de K, irá obter um outro elemento de K.
Essa é uma definição bastante informal, e consequentemente um pouco mais simples. Mas em livros de álgebra linear há definições bem mais rigorosas que inclusive mostram algumas propriedades que os elementos de K devem satisfazer.
-
anderson_wallace
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Seg Dez 30, 2013 17:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ciência e Tecnologia
- Andamento: cursando
 por Razoli » Qua Jan 08, 2014 19:57
por Razoli » Qua Jan 08, 2014 19:57
Então o corpo K é como se fosse uma regra que o conjunto V deve tomar?
Se K = R, e K assumir duas operações (+/-) o meu conjunto V deve satisfazer obrigatoriamente K, ai meu V é um espaço vetorial?
-
Razoli
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sáb Abr 06, 2013 15:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatistica
- Andamento: cursando
 por anderson_wallace » Qua Jan 08, 2014 20:59
por anderson_wallace » Qua Jan 08, 2014 20:59
Não exatamente, um corpo K não é uma regra que um dado espaço vetorial deve satisfazer.
Um corpo K é
conjunto de números reais ou complexos que deve satisfazer as seguintes propriedades:
1ª) Os números 0 e 1 estão em K;
2ª) Se

então x+y e x.y pertencem a K;
3ª) Se
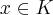
então o seu simétrico, isto é

;
4ª) Se
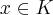
e
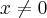
então o inverso
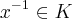
.
Já para verificar se V é um espaço vetorial vc não precisa verificar as propriedades do corpo numérico e sim as oito propriedades de espaço vetorial (que vc pode encontrar facilmente em qualquer livro), nessa situação o corpo K servirá basicamente para vc tomar elementos de K como escalares para testar as propriedades de espaço.
Por exemplo, umas das propriedades que um conjunto V qualquer deve satisfazer para ser um espaço vetorial sobre o corpo do números reais é a seguinte:

Note que o escalar

está no corpo, que neste caso é R.
-
anderson_wallace
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Seg Dez 30, 2013 17:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ciência e Tecnologia
- Andamento: cursando
 por Razoli » Qua Jan 08, 2014 21:52
por Razoli » Qua Jan 08, 2014 21:52
Hmmm então o K é nada mais que um conjunto que contém elementos, que podem ser complexos ou Reais, no qual é um corpo dos escalares, que ira satisfazer os axiomas escalares para verificar se um conjunto qualquer V é ou não um Espaço vetorial?
-
Razoli
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sáb Abr 06, 2013 15:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatistica
- Andamento: cursando
 por anderson_wallace » Qua Jan 08, 2014 22:04
por anderson_wallace » Qua Jan 08, 2014 22:04
Razoli escreveu:Hmmm então o K é nada mais que um conjunto que contém elementos, que podem ser complexos ou Reais
Até aí está certo, daí para frente não entendi muito bem, por isso não posso garantir, mas parece que vc está chegando a conclusão certa.
-
anderson_wallace
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Seg Dez 30, 2013 17:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ciência e Tecnologia
- Andamento: cursando
 por Razoli » Qui Jan 09, 2014 13:33
por Razoli » Qui Jan 09, 2014 13:33
Valeu por tudo, acabou minhas dúvidas!! Muito Obrigado por me auxiliar!!
-
Razoli
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sáb Abr 06, 2013 15:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatistica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Espaço vetorial
por amr » Sex Abr 01, 2011 15:30
- 4 Respostas
- 8194 Exibições
- Última mensagem por Rosi7

Sáb Mai 30, 2015 00:16
Introdução à Álgebra Linear
-
- Espaço vetorial
por oliveiramerika » Sáb Jan 19, 2013 10:03
- 1 Respostas
- 5939 Exibições
- Última mensagem por young_jedi

Dom Jan 20, 2013 09:29
Álgebra Linear
-
- Espaço Vetorial
por manuel_pato1 » Sáb Mar 02, 2013 20:03
- 0 Respostas
- 1869 Exibições
- Última mensagem por manuel_pato1

Sáb Mar 02, 2013 20:03
Álgebra Linear
-
- Espaço Vetorial
por erickm93 » Qui Out 17, 2013 16:48
- 0 Respostas
- 1709 Exibições
- Última mensagem por erickm93

Qui Out 17, 2013 16:48
Álgebra Linear
-
- [Sub-espaço vetorial]
por JauM » Qua Dez 04, 2013 14:15
- 2 Respostas
- 2162 Exibições
- Última mensagem por JauM

Qui Dez 05, 2013 14:37
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



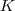 de números complexos (note que o conjunto dos reais também está contido em K) que é fechado em relação as operações elementares, ou seja, se vc somar, subtrair,multiplicar ou dividir (com divisor diferente de 0) elementos de K, irá obter um outro elemento de K.
de números complexos (note que o conjunto dos reais também está contido em K) que é fechado em relação as operações elementares, ou seja, se vc somar, subtrair,multiplicar ou dividir (com divisor diferente de 0) elementos de K, irá obter um outro elemento de K.

 então x+y e x.y pertencem a K;
então x+y e x.y pertencem a K;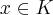 então o seu simétrico, isto é
então o seu simétrico, isto é  ;
;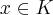 e
e 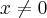 então o inverso
então o inverso 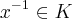 .
.
 está no corpo, que neste caso é R.
está no corpo, que neste caso é R.





 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.