Olá, tenho uma dúvida referente:
O QUE É esse CORPO "K" , onde o conjunto V esta sobre o mesmo, não estou entendendo o que é esse corpo! Alguém poderia me explicar de forma bastante intuitiva?



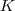 de números complexos (note que o conjunto dos reais também está contido em K) que é fechado em relação as operações elementares, ou seja, se vc somar, subtrair,multiplicar ou dividir (com divisor diferente de 0) elementos de K, irá obter um outro elemento de K.
de números complexos (note que o conjunto dos reais também está contido em K) que é fechado em relação as operações elementares, ou seja, se vc somar, subtrair,multiplicar ou dividir (com divisor diferente de 0) elementos de K, irá obter um outro elemento de K.

 então x+y e x.y pertencem a K;
então x+y e x.y pertencem a K;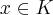 então o seu simétrico, isto é
então o seu simétrico, isto é  ;
;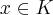 e
e 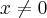 então o inverso
então o inverso 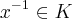 .
.
 está no corpo, que neste caso é R.
está no corpo, que neste caso é R.

Razoli escreveu:Hmmm então o K é nada mais que um conjunto que contém elementos, que podem ser complexos ou Reais


Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

