 por jricardo » Sáb Ago 17, 2013 01:13
por jricardo » Sáb Ago 17, 2013 01:13
Olá, estou estudando o livro Cálculo de George Thomas, edição 11°. Na página 205 deste livro, consegui entender o exemplo referente ao fólio de Descartes por meio da derivada implícita, porém, no final deste exemplo é apresentado uma outra forma de resolver o problema em questão, porém com o uso de uma fórmula para as três raízes de uma equação cúbica parecida com a fórmula quadrática
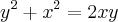
, que neste caso sería
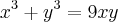
.
Neste exemplo é apresentado como resultado as seguintes equações:
![y = f(x) = \sqrt[3]{-\frac{{x}^{3}}{2} + \sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}}+\sqrt[3]{-\frac{{x}^{3}}{2}-\sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}} y = f(x) = \sqrt[3]{-\frac{{x}^{3}}{2} + \sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}}+\sqrt[3]{-\frac{{x}^{3}}{2}-\sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}}](/latexrender/pictures/31e811492174928eaab6e79030298789.png)
e
![y = \frac{1}{2}\left[-f(x)+\sqrt[2]{-3} \left(\sqrt[3]{-\frac{{x}^{3}}{2} + \sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}}-\sqrt[3]{-\frac{{x}^{3}}{2}-\sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}} \right) \right] y = \frac{1}{2}\left[-f(x)+\sqrt[2]{-3} \left(\sqrt[3]{-\frac{{x}^{3}}{2} + \sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}}-\sqrt[3]{-\frac{{x}^{3}}{2}-\sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}} \right) \right]](/latexrender/pictures/26765b3d4eeddd0138a8e0a8e58e90b7.png)
ou
![y = \frac{1}{2}\left[-f(x)-\sqrt[2]{-3} \left(\sqrt[3]{-\frac{{x}^{3}}{2} + \sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}}-\sqrt[3]{-\frac{{x}^{3}}{2}-\sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}} \right) \right] y = \frac{1}{2}\left[-f(x)-\sqrt[2]{-3} \left(\sqrt[3]{-\frac{{x}^{3}}{2} + \sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}}-\sqrt[3]{-\frac{{x}^{3}}{2}-\sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}} \right) \right]](/latexrender/pictures/0ff6ecdd8842db5587ac62d2a783d39c.png)
A dúvida é, como chegar a este resultado, pois o máximo que consegui foi:
![y = f(x) = \sqrt[3]{9xy - {x}^{3}} y = f(x) = \sqrt[3]{9xy - {x}^{3}}](/latexrender/pictures/a28b937ad2e750ebd4b1b3d696e81d09.png)
Alguém pode me ajudar.
Desde já, deixo o meu agradecimento.
-
jricardo
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Mar 31, 2013 22:21
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação cúbica
por Douglas16 » Ter Abr 09, 2013 15:24
- 1 Respostas
- 1046 Exibições
- Última mensagem por e8group

Ter Abr 09, 2013 20:38
Equações
-
- [EQUAÇÃO CUBICA] COMO RESOLVER ?
por slfdias » Qui Set 14, 2017 09:36
- 0 Respostas
- 1218 Exibições
- Última mensagem por slfdias

Qui Set 14, 2017 09:36
Equações
-
- Como encontrar as raízes da Equação Cúbica
por DHST » Seg Nov 14, 2011 15:06
- 4 Respostas
- 2373 Exibições
- Última mensagem por DHST

Qua Nov 16, 2011 17:15
Sistemas de Equações
-
- [Descobrir equação pela raiz]
por Mayra Luna » Qua Nov 21, 2012 17:59
- 2 Respostas
- 1466 Exibições
- Última mensagem por Mayra Luna

Qua Nov 21, 2012 21:10
Equações
-
- determinado pela equação cartesiana
por Neta Silva » Sex Mar 14, 2014 20:58
- 1 Respostas
- 1373 Exibições
- Última mensagem por Russman

Sex Mar 14, 2014 22:43
Introdução à Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
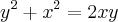 , que neste caso sería
, que neste caso sería 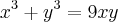 .
.![y = f(x) = \sqrt[3]{-\frac{{x}^{3}}{2} + \sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}}+\sqrt[3]{-\frac{{x}^{3}}{2}-\sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}} y = f(x) = \sqrt[3]{-\frac{{x}^{3}}{2} + \sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}}+\sqrt[3]{-\frac{{x}^{3}}{2}-\sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}}](/latexrender/pictures/31e811492174928eaab6e79030298789.png)
![y = \frac{1}{2}\left[-f(x)+\sqrt[2]{-3} \left(\sqrt[3]{-\frac{{x}^{3}}{2} + \sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}}-\sqrt[3]{-\frac{{x}^{3}}{2}-\sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}} \right) \right] y = \frac{1}{2}\left[-f(x)+\sqrt[2]{-3} \left(\sqrt[3]{-\frac{{x}^{3}}{2} + \sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}}-\sqrt[3]{-\frac{{x}^{3}}{2}-\sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}} \right) \right]](/latexrender/pictures/26765b3d4eeddd0138a8e0a8e58e90b7.png)
![y = \frac{1}{2}\left[-f(x)-\sqrt[2]{-3} \left(\sqrt[3]{-\frac{{x}^{3}}{2} + \sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}}-\sqrt[3]{-\frac{{x}^{3}}{2}-\sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}} \right) \right] y = \frac{1}{2}\left[-f(x)-\sqrt[2]{-3} \left(\sqrt[3]{-\frac{{x}^{3}}{2} + \sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}}-\sqrt[3]{-\frac{{x}^{3}}{2}-\sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}} \right) \right]](/latexrender/pictures/0ff6ecdd8842db5587ac62d2a783d39c.png)
![y = f(x) = \sqrt[3]{9xy - {x}^{3}} y = f(x) = \sqrt[3]{9xy - {x}^{3}}](/latexrender/pictures/a28b937ad2e750ebd4b1b3d696e81d09.png)

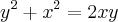 , que neste caso sería
, que neste caso sería 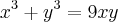 .
.![y = f(x) = \sqrt[3]{-\frac{{x}^{3}}{2} + \sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}}+\sqrt[3]{-\frac{{x}^{3}}{2}-\sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}} y = f(x) = \sqrt[3]{-\frac{{x}^{3}}{2} + \sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}}+\sqrt[3]{-\frac{{x}^{3}}{2}-\sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}}](/latexrender/pictures/31e811492174928eaab6e79030298789.png)
![y = \frac{1}{2}\left[-f(x)+\sqrt[2]{-3} \left(\sqrt[3]{-\frac{{x}^{3}}{2} + \sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}}-\sqrt[3]{-\frac{{x}^{3}}{2}-\sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}} \right) \right] y = \frac{1}{2}\left[-f(x)+\sqrt[2]{-3} \left(\sqrt[3]{-\frac{{x}^{3}}{2} + \sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}}-\sqrt[3]{-\frac{{x}^{3}}{2}-\sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}} \right) \right]](/latexrender/pictures/26765b3d4eeddd0138a8e0a8e58e90b7.png)
![y = \frac{1}{2}\left[-f(x)-\sqrt[2]{-3} \left(\sqrt[3]{-\frac{{x}^{3}}{2} + \sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}}-\sqrt[3]{-\frac{{x}^{3}}{2}-\sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}} \right) \right] y = \frac{1}{2}\left[-f(x)-\sqrt[2]{-3} \left(\sqrt[3]{-\frac{{x}^{3}}{2} + \sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}}-\sqrt[3]{-\frac{{x}^{3}}{2}-\sqrt[2]{\frac{{x}^{6}}{4}}-27{x}^{3}} \right) \right]](/latexrender/pictures/0ff6ecdd8842db5587ac62d2a783d39c.png)
![y = f(x) = \sqrt[3]{9xy - {x}^{3}} y = f(x) = \sqrt[3]{9xy - {x}^{3}}](/latexrender/pictures/a28b937ad2e750ebd4b1b3d696e81d09.png)

