 por xerebede » Qui Abr 04, 2013 17:23
por xerebede » Qui Abr 04, 2013 17:23
Olá, há questões que pedem o número de algarismos de um produto de dois ou mais fatores:
Há algum método que é utilizado para se determinar o número de algarismos de um produto de  fatores?Por exemplo:
fatores?Por exemplo:Quantos algarismos há no produto

?
Tentei resolver com exemplos numéricos menores, mas não consegui abstrair uma regularidade os testes que fiz:
Segue minha lógica: 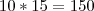

tem
2 casas decimais
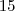
tem
2 casas decimais
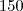
tem

casas decimais
Logo:

onde:

Número de algarismos do 1º fator

Número de algarismos do 2º fator

Número de algarismos Produto dos dois fatores
Porém, alguns produtos de 2 algarismos, em cada fator, resultam em números com 4 algarismos, tais como:
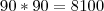
,

Matemática Base as vezes parece mais difícil do que problemas de geometria ou probabilidade, ou é só falta de habituação de fazer questões desse tipo.
Há algum método que é utilizado para se determinar o número de algarismos de um produto de  fatores?
fatores?No Aguardo...
-
xerebede
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Abr 04, 2013 16:26
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Informática
- Andamento: formado
 por DanielFerreira » Ter Abr 16, 2013 16:27
por DanielFerreira » Ter Abr 16, 2013 16:27
Xerebede,
boa tarde!
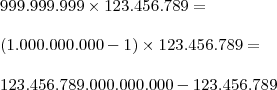
Logo, basta contar a quantidade de algarismos do maior número acima.
Daí,
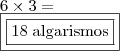
Espero ter ajudado!
Em caso de dúvidas, retorne!
Att,
Daniel.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por xerebede » Qui Abr 18, 2013 09:22
por xerebede » Qui Abr 18, 2013 09:22
Obrigado pela replica Danjr5!
Verifiquei e com seu desenvolvimento consegui resolver problemas envolvendo
noves. Porém, depois de alguns dias, com este tipo de solução vindo a cabeça a cada questão feita cheguei também a outro método. Segue:
Sabe-se que o minímo de algarismos que se pode ter é a soma do numero de algarismos das parcelas menos

. Para saber se um produto qualquer irá ultrapassar esse mínimo, basta multiplicar o ultimo algarismo do segundo fator pelo primerio fator, caso a multiplicação dos ultimos algarismos, do primeiro e segundo fator, exceda a casa das unidades, a quantidade de algarismos excedentes será somada ao tamanho do produto.
Exemplificando.

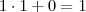
Não passa da casa das unidades, caracterizando tamanho mínimo:

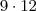

Passou da casa das unidades, portanto, o tamanho será o mínimo mais a quantidade de algarismos que vem após a casa das unidades:



Não passa da casa das unidades, caracterizando tamanho mínimo:
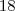
algarismos
-
xerebede
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Abr 04, 2013 16:26
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Informática
- Andamento: formado
 por DanielFerreira » Qui Abr 18, 2013 10:34
por DanielFerreira » Qui Abr 18, 2013 10:34
Ótimo raciocínio. Parabéns!!
Até a próxima!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Contagem - número algarismos página de livro
por remoreiraaa » Sáb Jan 02, 2010 22:43
- 2 Respostas
- 9876 Exibições
- Última mensagem por elsouza

Dom Jan 03, 2010 08:45
Álgebra Elementar
-
- [Aritmética] - Descobrir quantos algarismos tem um número.
por matano2104 » Qui Ago 29, 2013 18:30
- 1 Respostas
- 1871 Exibições
- Última mensagem por Russman

Qui Ago 29, 2013 22:07
Aritmética
-
- Produto escalar, Produto Vetorial e Produto Misto
 por fernando7 » Qua Mai 23, 2018 17:29
por fernando7 » Qua Mai 23, 2018 17:29
- 0 Respostas
- 4946 Exibições
- Última mensagem por fernando7

Qua Mai 23, 2018 17:29
Geometria Analítica
-
- ALGARISMOS DE 0 A 9
por Molina » Dom Jun 12, 2011 22:35
- 8 Respostas
- 6768 Exibições
- Última mensagem por tenebroso

Qua Dez 18, 2013 23:18
Desafios Difíceis
-
- Algarismos
por Valmel » Ter Out 23, 2012 18:23
- 1 Respostas
- 1686 Exibições
- Última mensagem por young_jedi

Ter Out 23, 2012 19:56
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 fatores?
fatores? ?
?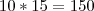
 tem 2 casas decimais
tem 2 casas decimais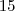 tem 2 casas decimais
tem 2 casas decimais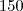 tem
tem  casas decimais
casas decimais
 Número de algarismos do 1º fator
Número de algarismos do 1º fator Número de algarismos do 2º fator
Número de algarismos do 2º fator Número de algarismos Produto dos dois fatores
Número de algarismos Produto dos dois fatores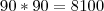 ,
, 
 fatores?
fatores?

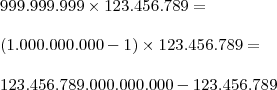
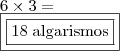

 . Para saber se um produto qualquer irá ultrapassar esse mínimo, basta multiplicar o ultimo algarismo do segundo fator pelo primerio fator, caso a multiplicação dos ultimos algarismos, do primeiro e segundo fator, exceda a casa das unidades, a quantidade de algarismos excedentes será somada ao tamanho do produto.
. Para saber se um produto qualquer irá ultrapassar esse mínimo, basta multiplicar o ultimo algarismo do segundo fator pelo primerio fator, caso a multiplicação dos ultimos algarismos, do primeiro e segundo fator, exceda a casa das unidades, a quantidade de algarismos excedentes será somada ao tamanho do produto.
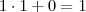 Não passa da casa das unidades, caracterizando tamanho mínimo:
Não passa da casa das unidades, caracterizando tamanho mínimo: 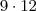
 Passou da casa das unidades, portanto, o tamanho será o mínimo mais a quantidade de algarismos que vem após a casa das unidades:
Passou da casa das unidades, portanto, o tamanho será o mínimo mais a quantidade de algarismos que vem após a casa das unidades: 

 Não passa da casa das unidades, caracterizando tamanho mínimo:
Não passa da casa das unidades, caracterizando tamanho mínimo: 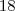 algarismos
algarismos

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.