Há algum método que é utilizado para se determinar o número de algarismos de um produto de
 fatores?
fatores?Por exemplo:
Quantos algarismos há no produto
 ?
?Tentei resolver com exemplos numéricos menores, mas não consegui abstrair uma regularidade os testes que fiz:
Segue minha lógica:
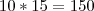
 tem 2 casas decimais
tem 2 casas decimais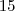 tem 2 casas decimais
tem 2 casas decimais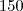 tem
tem  casas decimais
casas decimaisLogo:

onde:
 Número de algarismos do 1º fator
Número de algarismos do 1º fator Número de algarismos do 2º fator
Número de algarismos do 2º fator Número de algarismos Produto dos dois fatores
Número de algarismos Produto dos dois fatoresPorém, alguns produtos de 2 algarismos, em cada fator, resultam em números com 4 algarismos, tais como:
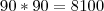 ,
, 
Matemática Base as vezes parece mais difícil do que problemas de geometria ou probabilidade, ou é só falta de habituação de fazer questões desse tipo.
Há algum método que é utilizado para se determinar o número de algarismos de um produto de
 fatores?
fatores?No Aguardo...


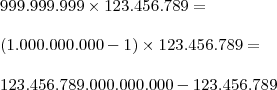
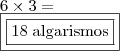

 . Para saber se um produto qualquer irá ultrapassar esse mínimo, basta multiplicar o ultimo algarismo do segundo fator pelo primerio fator, caso a multiplicação dos ultimos algarismos, do primeiro e segundo fator, exceda a casa das unidades, a quantidade de algarismos excedentes será somada ao tamanho do produto.
. Para saber se um produto qualquer irá ultrapassar esse mínimo, basta multiplicar o ultimo algarismo do segundo fator pelo primerio fator, caso a multiplicação dos ultimos algarismos, do primeiro e segundo fator, exceda a casa das unidades, a quantidade de algarismos excedentes será somada ao tamanho do produto.
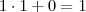 Não passa da casa das unidades, caracterizando tamanho mínimo:
Não passa da casa das unidades, caracterizando tamanho mínimo: 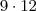
 Passou da casa das unidades, portanto, o tamanho será o mínimo mais a quantidade de algarismos que vem após a casa das unidades:
Passou da casa das unidades, portanto, o tamanho será o mínimo mais a quantidade de algarismos que vem após a casa das unidades: 

 Não passa da casa das unidades, caracterizando tamanho mínimo:
Não passa da casa das unidades, caracterizando tamanho mínimo: 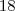 algarismos
algarismos