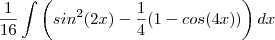Observei que há alguns erros em relação a sua solução ,alguns destes "erros" acredito que realmente seja "descuido" ao digitar .
Considere :
(i)
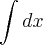
(ii)

(iii)
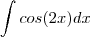
.
(iv)

.
No item (ii) e (iii) sua resolução está correta (por isso não vou comentar sobre eles) ,já em relação ao item (i) acredito que houve um "descuido" ao digitar o resultado da integral .Veja :

e não

.No item (iv) a resolução também está correta .Você utilizou a identidade
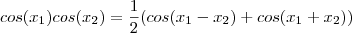
.
OBS_1 .: Recomendo que verfique atentamente tudo o que digitou e observe que há alguns erros em especial terceira , quarta etapa da solução .
Só acrescentando ,você perguntou se

.Resposta : Da forma que
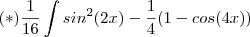
está escrito torna falso

.Mas se na verdade , a expressão digitada for

é verdadeiro

.
OBS_2 .: Sempre o "dx" acompanha o integrando .Assim ,
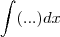
é o certo e não

.
Legenda : 
Além do problema de omitir o parênteses ()[que é importante para deixar claro que
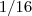
está multiplicando todas parcelas que estão dentro do parênteses] ,a expressão digitada apresenta o erro mencionado na
OBS_2 
Expressão digitada corrigida .
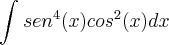
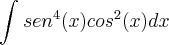
![\int_{}^{} {sen}^{2}(x) {[sen(x)cos(x)]}^{2}dx \int_{}^{} {sen}^{2}(x) {[sen(x)cos(x)]}^{2}dx](/latexrender/pictures/c127e0ca6f83c0a3459e82d022780ca6.png)
![{[sen(x)cos(x)]}^{2} {[sen(x)cos(x)]}^{2}](/latexrender/pictures/2d8a8462fbba78d85dc3cc119b93fbb2.png)
 que é justamente essa transformação que não entendi. Na integral fica
que é justamente essa transformação que não entendi. Na integral fica 


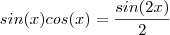 ,pois
,pois 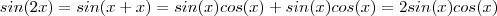 . Daí ,
. Daí , ![[sin(x)cos(x)]^2 = \left(\frac{sin(2x)}{2}\right)^2 = \frac{1}{4}sin^2(2x) [sin(x)cos(x)]^2 = \left(\frac{sin(2x)}{2}\right)^2 = \frac{1}{4}sin^2(2x)](/latexrender/pictures/83de7dc72db6df019b51f496136287aa.png) .
.
 (1.1) [Identidade trigonométrica fundamental]
(1.1) [Identidade trigonométrica fundamental]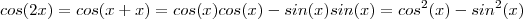 (1.2)
(1.2)  em função de
em função de 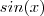 ,ao isolarmos
,ao isolarmos 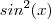 ,temos :
,temos :  (1.3)
(1.3)  que por
que por 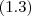 ,segue
,segue  .
. 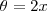 veremos que por (1.3)
veremos que por (1.3)  , ou seja , por (1.3)
, ou seja , por (1.3) 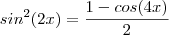 .
.
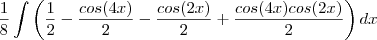
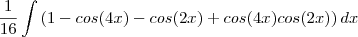 .
. .
.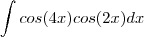 terá um pouco a mais de trabalho ,mas ela pode ser resolvida por integral por partes .Tente concluir ,se não conseguir post .
terá um pouco a mais de trabalho ,mas ela pode ser resolvida por integral por partes .Tente concluir ,se não conseguir post .
![\frac{1}{16}[1-\frac{sin(4x}{4}-\frac{sen(2x)}{2}+\frac{1}{2}\int_{}^{}cos(2x)+cos(6x)]= \frac{1}{16}[1-\frac{sin(4x}{4}-\frac{sen(2x)}{2}+\frac{1}{2}\int_{}^{}cos(2x)+cos(6x)]=](/latexrender/pictures/863caf21bb0ca02425424c1d7e654be4.png)
![\frac{1}{16}[1-\frac{sin(4x}{4}-\frac{sen(2x)}{2}+\frac{sin(2x)}{4}+\frac{sin(6x)}{12}]= \frac{1}{16}[1-\frac{sin(4x}{4}-\frac{sen(2x)}{2}+\frac{sin(2x)}{4}+\frac{sin(6x)}{12}]=](/latexrender/pictures/45ef2dd6838a0136271d808cd4b962c8.png)
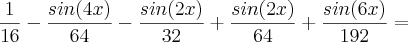
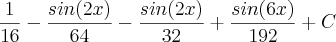
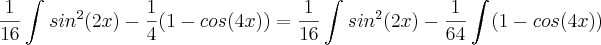
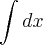

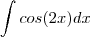 .
.  .
.  e não
e não  .No item (iv) a resolução também está correta .Você utilizou a identidade
.No item (iv) a resolução também está correta .Você utilizou a identidade 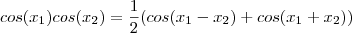 .
.  .Resposta : Da forma que
.Resposta : Da forma que 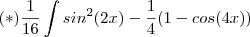 está escrito torna falso
está escrito torna falso  é verdadeiro
é verdadeiro  .
.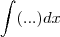 é o certo e não
é o certo e não  .
. Além do problema de omitir o parênteses ()[que é importante para deixar claro que
Além do problema de omitir o parênteses ()[que é importante para deixar claro que  está multiplicando todas parcelas que estão dentro do parênteses] ,a expressão digitada apresenta o erro mencionado na
está multiplicando todas parcelas que estão dentro do parênteses] ,a expressão digitada apresenta o erro mencionado na  Expressão digitada corrigida .
Expressão digitada corrigida .