por cleversonluizv » Qui Mar 14, 2013 15:23
por cleversonluizv » Qui Mar 14, 2013 15:23
Preciso da resolução desse problema.
No livro de chamada de uma sala de aula, há alunos que vão do número 1 ao 30. De quantas maneiras podemos
escolher 3 alunos de forma que a soma de seus números de chamada seja ímpar?
R: 2030
-
cleversonluizv
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Mar 08, 2013 14:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: formado
 por young_jedi » Sex Mar 15, 2013 11:36
por young_jedi » Sex Mar 15, 2013 11:36
a duas formas da soma ser um numero impar,
se os tres numeros forem impar ou se um for impar e os outors dois for par
de 1 a 30 temos 15 numeros pares e 15 impares,
1) para o primeiro caso, temos a combinção de 3 numeros em quinze

2) para o segundo caso nos temos as combinação de 2 numeros em quinze

mais cada uma dessas combinações vai ser combinada com um numero impar, como temos 15 numeros impares então

então o total de combinações vai ser a soma das combinações dos dois casos
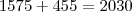
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Análise Combinatória
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [prova]
por Ge_dutra » Qui Mar 21, 2013 22:51
- 2 Respostas
- 1452 Exibições
- Última mensagem por Ge_dutra

Sex Mar 22, 2013 08:56
Cálculo: Limites, Derivadas e Integrais
-
- Prova 1 - 2002
 por admin » Sáb Jul 21, 2007 05:53
por admin » Sáb Jul 21, 2007 05:53
- 0 Respostas
- 1499 Exibições
- Última mensagem por admin

Sáb Jul 21, 2007 05:53
Cálculo Numérico e Aplicações
-
- Prova 1 - 2004
 por admin » Sáb Jul 21, 2007 05:55
por admin » Sáb Jul 21, 2007 05:55
- 0 Respostas
- 1600 Exibições
- Última mensagem por admin

Sáb Jul 21, 2007 05:55
Cálculo Numérico e Aplicações
-
- Prova 2 - 2004
 por admin » Sáb Jul 21, 2007 05:56
por admin » Sáb Jul 21, 2007 05:56
- 0 Respostas
- 1566 Exibições
- Última mensagem por admin

Sáb Jul 21, 2007 05:56
Cálculo Numérico e Aplicações
-
- exercicio de prova 3º ano
por hyenrique » Ter Fev 23, 2010 16:46
- 4 Respostas
- 5602 Exibições
- Última mensagem por hyenrique

Ter Fev 23, 2010 18:22
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.