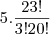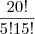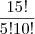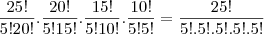por etocda » Ter Mar 12, 2013 21:30
por etocda » Ter Mar 12, 2013 21:30
Em um jogo de futebol entre 25 amigos que são divididos em times de 5 por sorteio com fichas com 5 cores diferentes. Neste jogo de futebol ninguém quer João em seu time, por este ser um baita perna-de-pau. Com estas informações quais as probabilidades de qualquer um dos 24 jogadores restante jogarem com João?
-
etocda
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Mar 12, 2013 21:14
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso técnico em edificações
- Andamento: cursando
 por young_jedi » Qui Mar 14, 2013 10:53
por young_jedi » Qui Mar 14, 2013 10:53
se o joão e outro cara estão no mesmo time então sobram tres vagas para os outros caras
ou seja

e cada uma desta combinações pode ocorrer em um time de uma das cinco cores
ou seja
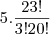
mais para cada uma destas combinações existe a combinação de cada um dos outros times de cada cor
para o time da segunda cor teremos
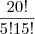
para o da terceira cor
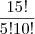
para o da quarta cor

e para a ultima cor somente 1 possivlidade que são o cinco jogadores que sobraram.
portanto o total de combinações em que joao e o outro cara estão no mesmo time é

agora vamos analisar o total de times que podem ser compostos com 25 jogadores em 5 cores diferentes
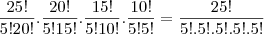
dividindo a primeira expressão pela segunda


-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por etocda » Dom Mar 17, 2013 13:58
por etocda » Dom Mar 17, 2013 13:58
Como a condição da questão seria a possibilidade de qualquer um dos jogadores jogarem com João.
Fiz da seguinte maneira:
C1,1 x C24,4 =10626 = combinações com joão no time.
C25,5 = 53130 combinações possiveis de 5 time.
Probabilidade= 10626/53130 = 20%.
por favor aponte onde errei.
-
etocda
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Mar 12, 2013 21:14
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso técnico em edificações
- Andamento: cursando
 por etocda » Dom Mar 17, 2013 14:02
por etocda » Dom Mar 17, 2013 14:02
young_jedi escreveu:se o joão e outro cara estão no mesmo time então sobram tres vagas para os outros caras
ou seja

e cada uma desta combinações pode ocorrer em um time de uma das cinco cores
ou seja
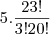
mais para cada uma destas combinações existe a combinação de cada um dos outros times de cada cor
para o time da segunda cor teremos
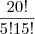
para o da terceira cor
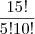
para o da quarta cor

e para a ultima cor somente 1 possivlidade que são o cinco jogadores que sobraram.
portanto o total de combinações em que joao e o outro cara estão no mesmo time é

agora vamos analisar o total de times que podem ser compostos com 25 jogadores em 5 cores diferentes
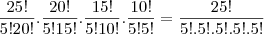
dividindo a primeira expressão pela segunda


Não compreendi o motivo pelo qual vc multiplicou o total desta forma: tex]\frac{25!}{5!20!}.\frac{20!}{5!15!}.\frac{15!}{5!10!}.\frac{10!}{5!5!}=\frac{25!}{5!.5!.5!.5!.5!}[/tex]
uma vez q os times são ajustados 5 a cinco, dum total de 25 jogadores. não seria o caso de uma combinação de 25 divididos 5 a cinco?
-
etocda
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Mar 12, 2013 21:14
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso técnico em edificações
- Andamento: cursando
 por young_jedi » Seg Mar 18, 2013 17:36
por young_jedi » Seg Mar 18, 2013 17:36
tipo o sorteio é com fichas de cores diferentes
vamaos supor que as fichas vermelhas são as primeiras
a combinção C(5,25) da o total de combinações para a ficha vermelha
agora a segunda cor é a verde como ja uitlizamos 5 jogadores para as vermelhas então nos temos
C(5,20) da o total de combinação das verdes
agora a terceira cor é a amarela como ja uitlizamos 5 jogadores para as vermelhas e cinco para as verdes então sobra 15 jogadores, então nos temos
C(5,15) da o total de combinação das amarelas
e assim por diante, então o multiplicação das combinações de cada cor fornece o total de times possiveis.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Probabilidade
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Probabilidade ] Jogo de futebol
por sanleovig » Seg Mai 06, 2013 15:19
- 1 Respostas
- 8473 Exibições
- Última mensagem por brunoiria

Sex Mai 10, 2013 14:07
Probabilidade
-
- Probabilidade no jogo de Poker
por jlmanetti » Sáb Out 10, 2009 22:42
- 2 Respostas
- 3544 Exibições
- Última mensagem por jlmanetti

Seg Out 12, 2009 12:47
Estatística
-
- [PROBABILIDADE] Jogo de Dados
por sweelinck » Qua Nov 23, 2011 02:47
- 3 Respostas
- 3395 Exibições
- Última mensagem por MarceloFantini

Qua Nov 23, 2011 16:35
Estatística
-
- [Probabilidade condicionada] Jogo de dados
por llbranco » Qui Abr 09, 2015 02:18
- 0 Respostas
- 2685 Exibições
- Última mensagem por llbranco

Qui Abr 09, 2015 02:18
Probabilidade
-
- problema do futebol
por hevhoram » Qui Jul 18, 2013 11:49
- 1 Respostas
- 13450 Exibições
- Última mensagem por IlgssonBraga

Qui Jul 18, 2013 13:36
Problemas do Cotidiano
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.