 por Tixa11 » Sáb Nov 10, 2012 12:26
por Tixa11 » Sáb Nov 10, 2012 12:26
Dada e função f(x)= log (arcsin (2x-1))=0, como calculo?
Eu chego até à parte arcsin(2x-1)=1 , mas depois não consigo passar daqui.
Alguém me pode ajudar e explicar? Por favor (:
-
Tixa11
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Sáb Nov 10, 2012 12:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bioquimica
- Andamento: cursando
 por MarceloFantini » Sáb Nov 10, 2012 13:37
por MarceloFantini » Sáb Nov 10, 2012 13:37
Temos
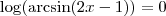
. Isso significa que

, mas o arco seno está definido em
![\left[ \frac{-\pi}{2}, \frac{\pi}{2} \right] \left[ \frac{-\pi}{2}, \frac{\pi}{2} \right]](/latexrender/pictures/628dbc55062fc566a170973d2557ccdc.png)
e logo
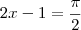
. Finalmente,
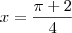
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Tixa11 » Dom Nov 11, 2012 20:07
por Tixa11 » Dom Nov 11, 2012 20:07
MarceloFantini escreveu:Temos
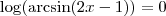
. Isso significa que

, mas o arco seno está definido em
![\left[ \frac{-\pi}{2}, \frac{\pi}{2} \right] \left[ \frac{-\pi}{2}, \frac{\pi}{2} \right]](/latexrender/pictures/628dbc55062fc566a170973d2557ccdc.png)
e logo
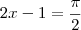
. Finalmente,
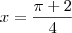
.
Não percebi muito bem :s
-
Tixa11
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Sáb Nov 10, 2012 12:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bioquimica
- Andamento: cursando
 por MarceloFantini » Seg Nov 12, 2012 05:05
por MarceloFantini » Seg Nov 12, 2012 05:05
O que, exatamente?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Tixa11 » Seg Nov 12, 2012 18:05
por Tixa11 » Seg Nov 12, 2012 18:05
MarceloFantini escreveu:O que, exatamente?
Ah, já percebi. Não estava a ver de onde vinha o

, mas já percebi.
Muito obrigado

-
Tixa11
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Sáb Nov 10, 2012 12:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bioquimica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Zeros da funcao
por sergiosilva » Qua Jan 05, 2011 22:59
- 3 Respostas
- 3863 Exibições
- Última mensagem por MarceloFantini

Qui Jan 06, 2011 21:13
Funções
-
- ZEROS DA FUNÇÃO
por Lenin » Sex Mai 31, 2013 03:10
- 3 Respostas
- 2145 Exibições
- Última mensagem por e8group

Sáb Jun 01, 2013 12:30
Funções
-
- [plano tangente a função de duas variaveis dada por função]
por isaac naruto » Qui Dez 31, 2015 16:35
- 0 Respostas
- 4587 Exibições
- Última mensagem por isaac naruto

Qui Dez 31, 2015 16:35
Cálculo: Limites, Derivadas e Integrais
-
- determinar os zeros da função
por anamendes » Dom Abr 29, 2012 12:37
- 1 Respostas
- 5815 Exibições
- Última mensagem por MarceloFantini

Dom Abr 29, 2012 14:06
Trigonometria
-
- DADA A FUNÇÃO
por SILMARAKNETSCH » Sex Nov 09, 2012 15:29
- 5 Respostas
- 2824 Exibições
- Última mensagem por SILMARAKNETSCH

Sex Nov 09, 2012 16:50
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



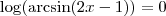 . Isso significa que
. Isso significa que  , mas o arco seno está definido em
, mas o arco seno está definido em ![\left[ \frac{-\pi}{2}, \frac{\pi}{2} \right] \left[ \frac{-\pi}{2}, \frac{\pi}{2} \right]](/latexrender/pictures/628dbc55062fc566a170973d2557ccdc.png) e logo
e logo 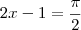 . Finalmente,
. Finalmente, 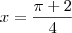 .
.

. Isso significa que
, mas o arco seno está definido em
e logo
. Finalmente,
.


 , mas já percebi.
, mas já percebi.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.