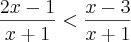 . Dê a resposta em termos de intervalo.
. Dê a resposta em termos de intervalo.é necessário que o denominador não seja nulo, então x > -1
no numerador fica assim:
2x-1<x-3
2x-x<-3+1
x<-2
S= {X e R / x > -1 ou x < -2 }
está correto a resolução e a resposta?

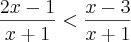 . Dê a resposta em termos de intervalo.
. Dê a resposta em termos de intervalo.
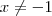 , apenas. Então a solução é
, apenas. Então a solução é 



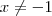 pois não se define divisão por zero. Agora, precisamos analisar dois casos: quando
pois não se define divisão por zero. Agora, precisamos analisar dois casos: quando 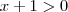 e quando
e quando  , ou seja,
, ou seja,  e
e 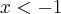 .
.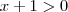 , multiplicando os dois lados da desigualdade por
, multiplicando os dois lados da desigualdade por  nos leva a
nos leva a  . Portanto, o primeiro conjunto é
. Portanto, o primeiro conjunto é 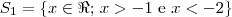 .
. , multiplicando os dois lados da desigualdade por
, multiplicando os dois lados da desigualdade por  nos leva a
nos leva a  . Como não existe nenhum número que satisfaça tal condição,
. Como não existe nenhum número que satisfaça tal condição,  .
. .
.

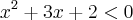



 você elimina o denominador e o numerador permanece o mesmo, fique atento à esse detalhe.
você elimina o denominador e o numerador permanece o mesmo, fique atento à esse detalhe.




 e
e 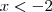 . Logo,
. Logo,  .
.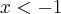 e
e  , levando à:
, levando à:



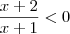



Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: